
|
| View previous topic :: View next topic |
| Author |
Message |
| PIsaacson
| | Joined: 17 Jan 2006 | | Posts: 47 | | : | | Location: Campbell, CA |
Items |
|
 Posted: Thu May 07, 2009 8:21 am Post subject: Using DLX for base/cover set logic eliminations Posted: Thu May 07, 2009 8:21 am Post subject: Using DLX for base/cover set logic eliminations |
 |
|
Rather than using Knuth's Dancing Links (DLX) implementation of his Algorithm X to competely solve a sudoku puzzle, I am instead going to discuss how to use DLX to generate all possible covers sets for a given base set.
Some preliminary requirements:
1) Download libexact and read the PDF manual. http://www.cs.helsinki.fi/u/pkaski/libexact/libexact-1.0.tar.gz
2) Read Allan Barker's brief introduction to set/link-set logic. http://sudokuone.com/sweb/guide.htm
3) Basic knowledge of C/C++ and STL is important, but not necessarily critical.
The base/cover algorithm requires some outside method to discover/generate a base set. Currently, I'm using doubly-linked ALSs to generate a vector describing all the cells of both ALSs, but you can use whatever technique you want to generate such lists. However, the following code only works well for rank-0 logical structures, so if you want rank-1 chains etc, you'll have to adjust the filter to allow base+1 sized solutions, modify the elimination code to correctly test the overlap counts, and probably switch from cell base sets to lists of the actual sets used to link candidates.
Basically the technique works like this:
1) Find any interesting set of cells to examine. This becomes the base set.
2) Setup the DLX problem using the libexact (modified) API.
3) Execute libexact exact_solve to find all valid combinations of rows/cols/boxes that exactly cover the base cells.
4) For each solution, any outside candidate contained in a cover set but not in a base set can be eliminated.
This is similar to fishing algorithms that use base/cover sets for single digit analysis. In fact, I adapted it from my experimental fishing engine that also uses DLX in this manner. Here, it is being used in a more general fashion.
So, on to the code (written in C++ and depending heavily on STL):
| Code: | int base_filter (void *param, int sz, const int *soln, int col)
{
bitset<m_cols> *set_map = (bitset<m_cols> *) param;
return (set_map->_Unchecked_test (col) == 0);
}
int level_filter (void *param, int sz, const int *soln)
{
int max_sz = (int) param;
return (sz <= max_sz); // exact level_filter skips any solutions when sz > max_size from param when registered
}
int do_base_cover (bitset<m_cells> *sloc_map, bitset<m_rows> *updt_map, grid_t *grid, char *caller)
{
exact_t *e = ge; // pre-allocated in initialization code exact_t *ge = exact_alloc ();
exact_reset (e); // new call for a fast re-initialization of the exact_t structure
cand_map.reset (); // STL bitset<729> for defining possible candidates to eliminate
base_set.reset (); // STL bitset<729> for defining our input bitset based on the bitset<81> sloc_map cells
set_map.reset (); // STL bitset<324> for testing whether or not we've encountered a new cover set
int nh = 0; // counter for row/col headers used for new call exact_declare to setup our DLX problem
int ne = 0; // counter for entry headers used for new call exact_declare
int bc = sloc_map->count (); // Get the number of cells (base count)
int update = 0; // track how many updates (eliminations) were performed
// Scan our current PM grid to initialize the base_set and cand_set, plus build the row/col headers and entries
for (int n = 0; n < m_cells; n++) // m_cells = 81
{
if (grid->cell[n/m_n][n%m_n].digit > 0) // check to see if the cell is already solved
continue;
int r = n/m_n; // compute row
int c = n%m_n; // compute col
int b = rc2b[r][c]; // lookup box
int mbits = grid->cell[r][c].mbits; // fetch the current PM candidates for this cell
for (int d = 0; d < m_n; d++) // m_n = 9 so scan all the digits
{
if ((mbits & (1 << d)) == 0) // test if candidate d is set
continue;
int vx = NRC2V (d, r, c); // convert digit/row/col to NRC[729] address vx = r*81+c*9+d
cand_map[vx] = 1; // assign this as a valid candidate for potential elimination
if (sloc_map->_Unchecked_test (n) == 0) // test if this is one of our base cells
continue; // no - then skip the DLX row/col/entry setup
base_set[vx] = 1; // yes - assign this as a valid base set candidate
// Compute constraint indexes for this candidate
int nx = r*m_n+c; // RC space index as a constraint (first 81)
int rx = r*m_n+d + m_cells; // RN space index as a constraint (second 81)
int cx = c*m_n+d + m_cells*2; // CN space index as a constraint (third 81)
int bx = b*m_n+d + m_cells*3; // BN space index as a constraint (forth 81)
if (set_map[nx] == 0) // Test if this is the first time we saw this RC cell
{
set_map[nx] = 1;
// e_headers[nh++] = (TYPE_COL << 16 | nx); // Do nothing - may need this later for bases other than cells
}
if (set_map[rx] == 0) // Test is this is the first time we saw this RN entry
{
set_map[rx] = 1;
e_headers[nh++] = (TYPE_COL << 16 | rx); // Yes - setup the correct TYPE_COL header
}
if (set_map[cx] == 0) // Test if this is the first time we saw this CN
{
set_map[cx] = 1;
e_headers[nh++] = (TYPE_COL << 16 | cx); // Yes - setup the correct TYPE_COL header
}
if (set_map[bx] == 0) // Test if this is the first time we saw this BN
{
set_map[bx] = 1;
e_headers[nh++] = (TYPE_COL << 16 | bx); // Yes - setup the correct TYPE_COL header
}
e_headers[nh++] = (TYPE_ROW << 16 | vx); // Now setup the correct TYPE_ROW header
// e_entries[ne++] = (vx << 16) | nx; // Do nothing - may need this later for bases other than cells
e_entries[ne++] = (vx << 16) | rx; // Add the ROW/COL RN entry
e_entries[ne++] = (vx << 16) | cx; // Add the ROW/COL CN entry
e_entries[ne++] = (vx << 16) | bx; // Add the ROW/COL BN entry
}
}
// The DLX row/col headers and entries have been initialized - call exact_declare to setup the problem
int status = exact_declare (e, nh, ne, e_headers, e_entries); // new call that eliminates the multiple exact_declare_xxx calls
if (status) // all the calls (most of them anyway) now return status
{
printf ("do_base_cover - exact_declare failed with error %d\n", status);
exit (1);
}
int sc; // exact_solve count for number of entries the following vector
const int *s; // exact_solve solution vector
// exact_filter (e, base_filter, &set_map); // Do nothing - base filter not currently used
exact_level (e, level_filter, (void *) bc); // Install the level filter to restrict solutions to same sized base and cover sets
int ec = 0; // Track solution counter
// Execute the DLX and find all exact cover solutions
while (s = exact_solve (e, &sc)) // Standard exact_solve loop - returns NULL for no/last solution
{
link_set.reset (); // STL bitset<729> used for the union of all the cover sets
for (int n = 0; n < sc; n++) // sc contains the number of entries in the solution stack s
link_set |= m_covers->cover[s[n]].index; // m_cover is a table of 324 bitset<729> defining the 9 peers for the s[n] cover set
int changed = 0; // initialize the changed switch
memset (c_counts, 0, sizeof (c_counts)); // initialize the 729 cover counters
// Compute the cover counts for each NRC entry in the base_set and cand_set maps
for (int vx = 0; vx < m_rows; vx++) // m_rows = 729
{
if (base_set[vx]) // decrement cover count if this is in the base set
c_counts[vx]--;
if (link_set[vx] && cand_map[vx]) // increment cover count if this is in the candidate set and in the solution cover set
c_counts[vx]++;
}
// Test the cover counts for any eliminations due to this solution
for (int vx = 0; vx < m_rows; vx++)
{
if (c_counts[vx] != 0) // used to be (c_counts[vx] < 0 || c_counts[vx] > (sc - bc)) where sc - bc = fin count
{
int r = V2R (vx); // compute row = vx/81
int c = V2C (vx); // compute col = vx/9 & 0x1ff
int d = V2N (vx); // compute digit = vx%9
int change = update_mbit (d, r, c, grid); // see if we can eliminate this candidate (may already be done if change = 0)
update += change; // increment our update count (if any)
changed += change; // increment out changed count (if any)
if (change) // set our updated map for generating an xsudo sud case
updt_map->_Unchecked_set (vx);
if (sw_xverbose || sw_verbose && change) // generate a log entry for the elimination, if requested
{
printf ("%s - reducing r%dc%d.%s by <%d> base/cover\n", caller, r+1, c+1,
int2bin (grid->cell[r][c].mbits | (1 << d)), d+1);
}
}
}
if (sw_xverbose || sw_verbose && changed) // generate a log entry for the base/cover, if requested and any eliminations
{
printf ("%s - base/cover %s %s\n", caller, bs2bin (sloc_map, bc), cs2bin (s, sc));
}
}
return (update); // return the number of updates along with the updated map positions
}
|
If there is any interest, I'll post the modified libexact code as well as the driver code that takes a set of cells and generates multiple calls to do_base_cover for all possible combinations.
I'm hoping other programmers will become likewise interested in coding better base/cover analysis code that we can all share. Obviously there are many parts missing, but this is just a "teaser" and I'll release all the code embedded in my testbed ALS engine along with the code to generate sud case collections.
Cheers,
Paul
[edit] eliminated line numbers and disabled HTML to correct code presentation errors
Last edited by PIsaacson on Sat May 09, 2009 9:11 am; edited 2 times in total |
|
| Back to top |
|
 |
| PIsaacson
| | Joined: 17 Jan 2006 | | Posts: 47 | | : | | Location: Campbell, CA |
Items |
|
 Posted: Thu May 07, 2009 8:27 am Post subject: Posted: Thu May 07, 2009 8:27 am Post subject: |
 |
|
Updated build files for my testbed ALS engine:
Makefile.txt needs to be renamed to Makefile and all the others need to be placed in the same directory for correct building. I'm now using the mingw compilers under cygwin, so this should build correctly on just mingw.
http://pisaacson.fileave.com/Bernhard/Makefile.txt
http://pisaacson.fileave.com/Bernhard/combination.h
http://pisaacson.fileave.com/Bernhard/exact.h
http://pisaacson.fileave.com/Bernhard/sudoku.h
http://pisaacson.fileave.com/Bernhard/exact.cpp
http://pisaacson.fileave.com/Bernhard/sudoku.cpp
Pre-built library and executable
http://pisaacson.fileave.com/Bernhard/libexact.a
http://pisaacson.fileave.com/Bernhard/sudoku.exe
You should re-make the executable if you have the correct cygwin/mingw environment, then test using:
sudoku -bvgw -Xprsak -A9 -B0 -K2 -T-1 royle17.txt royle17.sud > royle17.log
This assumes you have downloaded the new 48010 royle17 collection into the current working directory from http://people.csse.uwa.edu.au/gordon/sudoku17
The command will run the ALS engine and locate all doubly-linked ALSs and Death Blossoms and generate an Xsudo collection in royle17.sud with the output logged in royle17.log
If all goes well, you should match (use "tail -16 royle17.log") the following statistics for the updates/call and % eff. The others depend upon the speed of the processor, but should be similar if normalized. | Code: | Puzzle call statistics:
do_pinnings updates/calls 64/6 1066.67% eff 0.1539 msec tot 0.0257 msec/call 0.0024 msec/update
Puzzle 48010 took 0.2137 msec for 1 solution(s)
Sudoku final statistics:
tot_pinnings updates/calls 3069183/476098 644.65% eff 16025.4457 msec tot 0.0337 msec/call 0.0052 msec/update
tot_restrictions updates/calls 341490/52473 650.79% eff 2683.6008 msec tot 0.0511 msec/call 0.0079 msec/update
tot_subsets updates/calls 139002/20415 680.88% eff 2054.8852 msec tot 0.1007 msec/call 0.0148 msec/update
tot_alschains updates/calls 45815/10768 425.47% eff 783604.2690 msec tot 72.7716 msec/call 17.1037 msec/update
tot_deathblossom updates/calls 77352/4107 1883.42% eff 225936.5771 msec tot 55.0126 msec/call 2.9209 msec/update
tot_dlx updates/calls 87/87 100.00% eff 78.2792 msec tot 0.8998 msec/call 0.8998 msec/update
C:\home\paul\bernhard\sudoku.exe -bvgw -Xprsak -A9 -B0 -K2 -T-1 royle17.txt royle17.sud |
I don't have a really fast cpu (old AMD X2 4200), so the above batch run takes somewhere between 12 and 15 minutes depending on what else I'm doing while the test is running.
I use cygwin and the WXDevCPP MinGW IDE. I'll post instructions on how to download these as soon as I can figure out a minimal install. Alternately, you could just install the full cygwin package, but that's really overkill unless you want to play with X-Windows, which is actually very cool and really makes you feel like you're running a Posix OS. |
|
| Back to top |
|
 |
| PIsaacson
| | Joined: 17 Jan 2006 | | Posts: 47 | | : | | Location: Campbell, CA |
Items |
|
 Posted: Thu May 07, 2009 8:28 am Post subject: Posted: Thu May 07, 2009 8:28 am Post subject: |
 |
|
For those who may have generate the above royle17.sud file and attempted to directly load it into Xsudo, it won't work because there are 62561 cases in one file. To circumvent this and to match Allan's new 2000 case limit, I have a small program that reads large sud collections, sorts them based on the keys that I have internally stored in the collection (see write_xsudo), then breaks them up into multiple 2000 max chunks.
Download: http://pisaacson.fileave.com/Bernhard/sortsud.cpp
Place it in the same directory as the other files and compile with:
g++ -O -I. sortsud.cpp -o sortsud
Execute as sortsud <filename> as in:
sortsud royle17.sud
Again, if you've been following along, this will generate 32 output files with the following output: | Code: | 70> sortsud royle17.sud
there are 62561 cases in this file
royle17 - output root
Opening file royle17_1.sud
Opening file royle17_2.sud
Opening file royle17_3.sud
Opening file royle17_4.sud
Opening file royle17_5.sud
Opening file royle17_6.sud
Opening file royle17_7.sud
Opening file royle17_8.sud
Opening file royle17_9.sud
Opening file royle17_10.sud
Opening file royle17_11.sud
Opening file royle17_12.sud
Opening file royle17_13.sud
Opening file royle17_14.sud
Opening file royle17_15.sud
Opening file royle17_16.sud
Opening file royle17_17.sud
Opening file royle17_18.sud
Opening file royle17_19.sud
Opening file royle17_20.sud
Opening file royle17_21.sud
Opening file royle17_22.sud
Opening file royle17_23.sud
Opening file royle17_24.sud
Opening file royle17_25.sud
Opening file royle17_26.sud
Opening file royle17_27.sud
Opening file royle17_28.sud
Opening file royle17_29.sud
Opening file royle17_30.sud
Opening file royle17_31.sud
Opening file royle17_32.sud
71> |
The cases are sorted by descending number of eliminations, ascending number of base cells, ascending puzzle number, and ascending step within puzzle. The first one contains the (debatably) more interesting ALSs/DBs. The eliminations are flagged with a small "x" so it is easy to check whether or not the base/cover algorithm agrees with Allan's Xsudo found eliminations. There is a deliberate "bug" in capturing the exact grid position so sometimes there are many eliminations listed that were found due to prior ALSs/DBs. |
|
| Back to top |
|
 |
| PIsaacson
| | Joined: 17 Jan 2006 | | Posts: 47 | | : | | Location: Campbell, CA |
Items |
|
 Posted: Thu May 07, 2009 9:02 am Post subject: Posted: Thu May 07, 2009 9:02 am Post subject: |
 |
|
Setting up a cygwin environment - read the installation instructions from http://cygwin.com/
I'm running the beta 1.7 cygwin install from http://cygwin.com/setup-1.7.exe
You'll need to manually select the following packages: | Code: | [Devel] binutils
boost
gcc-core
gcc-g++
gcc-mingw-core
gcc-mingw-g++
gdb
libboost
libgcc1
libstdc++6
libtool
make
mingw-runtime
The following editors are optional if you have some favorite Windows source code editor. Otherwise, I recommend at least trying Vim or Joe.
[Editors] hexedit
vim
emacs - It's not just an editor, it's a way of life...
joe
ted |
The WXDev-C++ IDE can be found at http://wxdsgn.sourceforge.net/
This is a very nice/free IDE for developing Windows C/C++ applications using the MinGW framework, but there's a steep learning curve if you really want to code using wxWidgets. I'm using this to develop a sudoku helper (not a solver), but it can compile the testbed pretty easily as well. If anyone is interested in going this route, I'll post details on how to setup the project. |
|
| Back to top |
|
 |
| PIsaacson
| | Joined: 17 Jan 2006 | | Posts: 47 | | : | | Location: Campbell, CA |
Items |
|
 Posted: Thu May 07, 2009 9:29 am Post subject: Posted: Thu May 07, 2009 9:29 am Post subject: |
 |
|
The above posting were originally posted on http://www.sudoku.com/boards/viewtopic.php?t=6694
There was no response/interest on the Players Forum, so perhaps I should have posted here first? Regardless, there are many discussions on the Players Forum that include various base/cover diagrams. So for the highly self-motivated individuals, I recommend studying any (if not all) of Allan Barker's postings. It's the implementation of his theory that I'd like to explore from a design/coding POV.
Cheers,
Paul |
|
| Back to top |
|
 |
| PIsaacson
| | Joined: 17 Jan 2006 | | Posts: 47 | | : | | Location: Campbell, CA |
Items |
|
 Posted: Fri May 08, 2009 8:56 pm Post subject: Posted: Fri May 08, 2009 8:56 pm Post subject: |
 |
|
I feel compelled to issue this disclaimer: My ALS engine is not intended to be used as a solver.
It is a testbed for locating various types of ALS chains and Death Blossoms and investigating the associated base/cover logic. Solving a puzzle to completion, while interesting and often possible, is not its main mission. The included techniques are present to bring puzzles to a known quasi-SSTS condition for large collections and/or puzzles not otherwise presented as PM grids after SSTS. With that proviso having been disclosed, it is still extraordinary how powerful ALS/DB can be in terms of solving puzzles without resorting to other higher level techniques. |
|
| Back to top |
|
 |
| PIsaacson
| | Joined: 17 Jan 2006 | | Posts: 47 | | : | | Location: Campbell, CA |
Items |
|
 Posted: Wed May 13, 2009 8:12 pm Post subject: Posted: Wed May 13, 2009 8:12 pm Post subject: |
 |
|
| Code: | 008700025000000900900600040009540060035000410476120000090005008003000000600001200
+-----------------------+----------------------+------------------------+
| (+3-1) 146 8 | 7 19-3 49 | (16) 2 5 |
| 57-123 12456 124-7 | 2348 1358 248 | 9 378 (1367) |
| 9 125 12-7 | 6 1358 28 | 378-1 4 (137) |
+-----------------------+----------------------+------------------------+
| (128) 12-8 9 | 5 4 378 | 378 6 (237) |
| (28) 3 5 | 89 6789 6789 | 4 1 (279) |
| 4 7 6 | 1 2 389 | 358 358-9 (39) |
+-----------------------+----------------------+------------------------+
| (12-7) 9 124-7 | 234 367 5 | 1367 37 8 |
| 5-1278 12458 3 | 2489 6789 246789 | 1567 579 16-479 |
| 6 58-4 (+7-4) | 389-4 389-7 1 | 2 359-7 (+4-379) |
+-----------------------+----------------------+------------------------+
1 (1 33 Candidates, Raw Rank = 6 (linksets - sets)
12 Sets = {1457N1 9N3 1N7 234569N9}
18 Links = {3r1 47r9 128c1 7c3 379c9 3b1 16b3 8b4 29b6 7b7 4b9}
27 Eliminations, 3 Assignments -->
r8c1<>1278, r9c234<>4, r9c589<>7, r237c3<>7, r2c1<>123, r8c9<>479,
r9c9<>39, r1c1<>1, r1c5<>3, r3c7<>1, r4c2<>8, r6c8<>9, r7c1<>7,
r1c1=3, r9c9=4, r9c3=7 |
| Code: | 29> sudoku -bvweg -Xprsak -A9 -B4 -P -T-1 alschain_001.pm alschain_001.sud
Puzzle: ..87...25......9..9..6...4...954..6..35...41.47612.....9...5..8..3......6....12.. puzzle 1 alschain_001.pm
13 146 8 |7 139 49 |16 2 5
12357 12456 1247 |2348 1358 248 |9 378 1367
9 125 127 |6 1358 28 |1378 4 137
--------- --------- ---------+--------- --------- ---------+--------- --------- ---------
128 128 9 |5 4 378 |378 6 237
28 3 5 |89 6789 6789 |4 1 279
4 7 6 |1 2 389 |358 3589 39
--------- --------- ---------+--------- --------- ---------+--------- --------- ---------
127 9 1247 |234 367 5 |1367 37 8
12578 12458 3 |2489 6789 246789 |1567 579 14679
6 458 47 |3489 3789 1 |2 3579 3479
do_alschains - graph contains 225 vertices and 948 edges
do_alschains - reducing r1c5.<139> by <3>
do_alschains - reducing r2c1.<12357> by <3>
do_alschains - reducing r2c1.<1257> by <1> base/cover
do_alschains - reducing r2c1.<257> by <2> base/cover
do_alschains - reducing r3c7.<1378> by <1> base/cover
do_alschains - reducing r7c3.<1247> by <7> base/cover
do_alschains - reducing r8c1.<12578> by <1> base/cover
do_alschains - reducing r8c1.<2578> by <2> base/cover
do_alschains - reducing r8c1.<578> by <7> base/cover
do_alschains - reducing r8c1.<58> by <8> base/cover
do_alschains - reducing r8c9.<14679> by <7> base/cover
do_alschains - reducing r8c9.<1469> by <9> base/cover
do_alschains - reducing r9c2.<458> by <4> base/cover
do_alschains - reducing r9c4.<3489> by <4> base/cover
do_alschains - base/cover {1n17 2n9 3n9 4n19 5n19 6n9 7n1 9n39} {3r1 4r9 128c1 2379c9 16b3 7b7}
do_alschains - reducing r4c2.<128> by <8> base/cover
do_alschains - base/cover {1n17 2n9 3n9 4n19 5n19 6n9 7n1 9n39} {3r1 4r9 12c1 2379c9 16b3 8b4 7b7}
do_alschains - als+[5x7/8] r1c1.<n13> -1- r1c7.<n16> -16- r234569c9.<n1234679> -4- r9c3.<n47> -7- r1457c1.<n12378> |
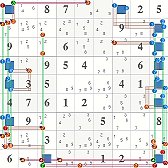
The example ALS chain r1c1 -1- r1c7 -16- r234569c9 -4- r9c3 -7- r1457c1 produces only 2 eliminations from the standard ALS rules. But when subjected to base/cover analysis, the ALS structure as a group produces 13 additional elimination just from my ALS engine's simple base/cover algorithm. Allan's Xsudo finds an incredible 27 eliminations and 3 assignments from the same structure. This pretty clearly demonstrates the "power" of Allan Barker's set/link-set theory.
If you have downloaded the code, create a file (alschain_001.pm below) containing the PM grid above and issue the following command:
sudoku -bvegw -Xprsa -A9 -B4 -P -T-1 alschain_001.pm alschain_001.sud
The ALS engine will create the alschain_001.sud file containing all the discovered ALS chains for analysis in Xsudo. For the adventurous, experiment with various -B<n> sized chain limits to see the impact of restricting ALS chain length. The valid values for -B range from 0 for chains with 2 ALSs to 32 for really long ALS chains with upto 34 ALSs. |
|
| Back to top |
|
 |
| nukefusion
| | Joined: 27 Jun 2009 | | Posts: 22 | | : | |
Items |
|
 Posted: Tue Aug 11, 2009 9:50 am Post subject: Posted: Tue Aug 11, 2009 9:50 am Post subject: |
 |
|
Hi Paul,
It appears I'm rather late stumbling over this thread. Thanks for posting this stuff up as I'm currently looking at Death Blossoms myself. I've found that discovering the ALS's and matching up potential stems is easy, but the slow part comes when testing the various combinations of stem cell/petals to see which are valid (i.e. no overlapping cells between ALS's) and which produce any useful eliminations.
I think I'm going to have to re-read your posts a few times in order to gain even a small understanding of how it all fits together but it certainly looks very interesting! |
|
| Back to top |
|
 |
| PIsaacson
| | Joined: 17 Jan 2006 | | Posts: 47 | | : | | Location: Campbell, CA |
Items |
|
 Posted: Tue Aug 11, 2009 7:08 pm Post subject: Posted: Tue Aug 11, 2009 7:08 pm Post subject: |
 |
|
Matt,
I have the ALS and DB engine in a somewhat simpler form in pascal at http://pisaacson.fileave.com/Sudoku/sudoku.zip
There has been no activity/response for this thread (other than yours!), so I have not kept the code current with my latest implementation of base/cover logic ala Allan Barker's SLG theory. If you are just interested in ALSs and DBs, then the base/cover logic is probably overkill anyway and the pascal version is more up-to-date with my full solver.
Cheers,
Paul |
|
| Back to top |
|
 |
|
|
You cannot post new topics in this forum
You cannot reply to topics in this forum
You cannot edit your posts in this forum
You cannot delete your posts in this forum
You cannot vote in polls in this forum
|

Powered by phpBB © 2001, 2005 phpBB Group
Igloo Theme Version 1.0 :: Created By: Andrew Charron |




