
|
| View previous topic :: View next topic |
| Author |
Message |
| chuckfresno
| | Joined: 16 Jun 2005 | | Posts: 39 | | : | |
Items |
|
 Posted: Sun Jul 24, 2005 5:52 am Post subject: A variety of Sudoku Variants Posted: Sun Jul 24, 2005 5:52 am Post subject: A variety of Sudoku Variants |
 |
|
These images are also here:
http://sudokuvariants.blogspot.com/ ]
The names are merely descriptive. I don't know what they may actually be named. They are all from Japanese magazines 5 to 10 years old.

Irregular groups.
Very common variant. Sub-groups are irregular instead of 3x3 boxes. These irregular groups may or may not be symmetrical.
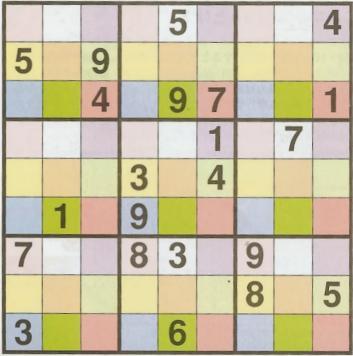
Disjoint groups
In addition to the standard 27 groups (rows, columns, boxes), there are 9 more "disjoint" groups, each shaded on of 9 colors. All digits on one color must be different.

Diagonals
The two main diagonals must also contain each digit.

Extra groups
In addition to the standard 27 groups (rows, columns, boxes), there are 4 more groups, shown with shading. The number of auxillary groups varies.

Even and Odd
Dark shaded cells will have even numbers, light will have odd.

Overlapping plus diagonal groups
These overlapping puzzles include diagonal groups -- the 4 main diagonals must have one of each digit.
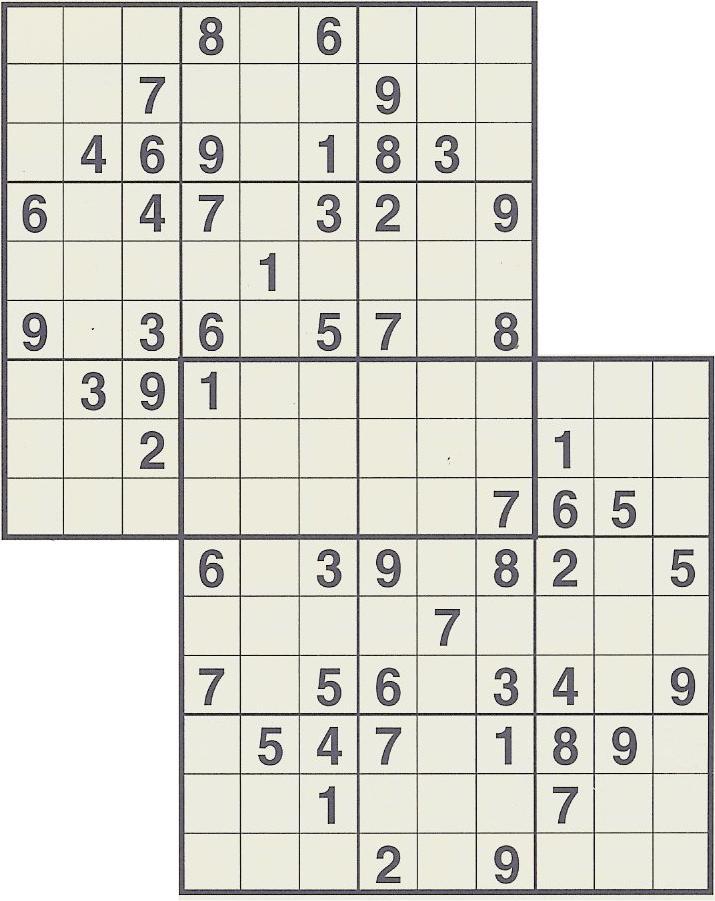
Overlapping
A variation from the standard overlapping puzzle
Overlapping
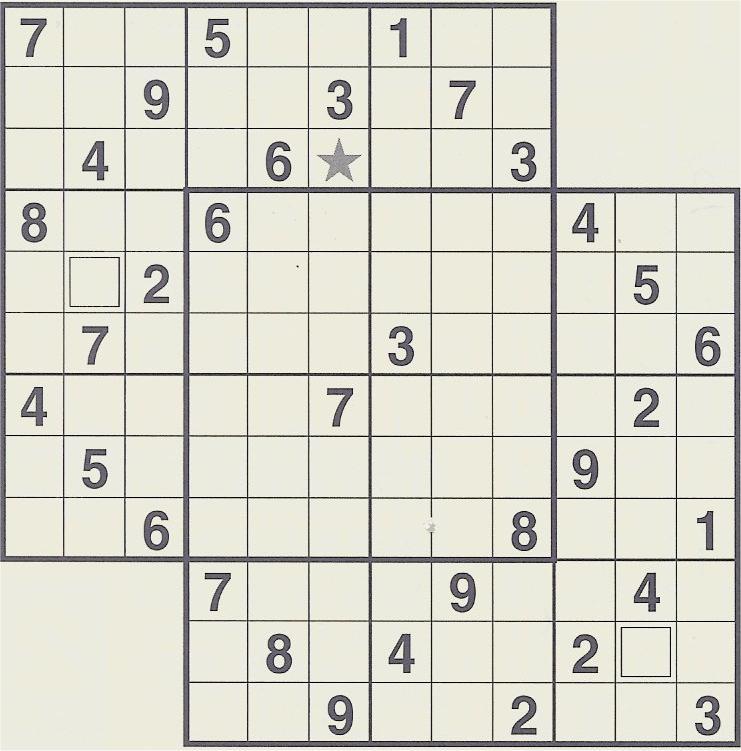
A variation from the standard overlapping puzzle. Cells marked with squares are not used in solving, only for sending in solution. Purpose for STAR cell is unknow. I'm guessing it's a hint -- either something like START HERE -- or possible there is an actual clue somewhere in the magazine. I don't know; I don't speak Japanese.
Three overlapping -- tight
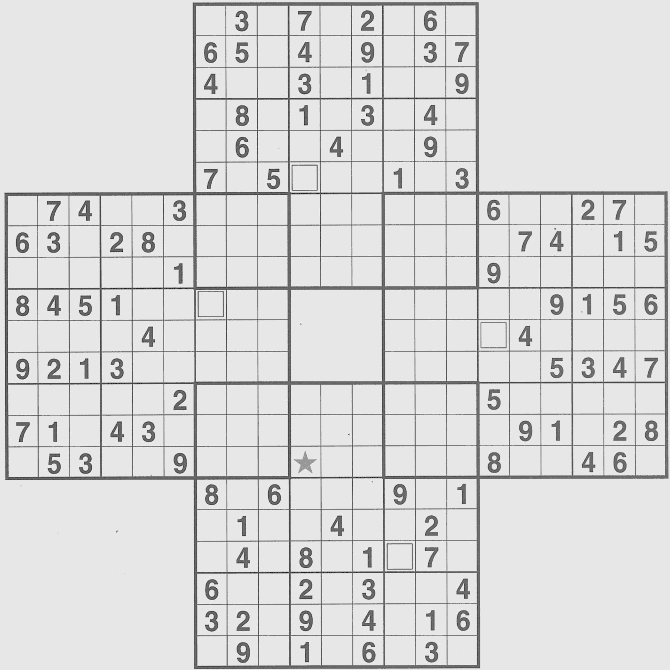
Four Overlapping, standard
Again, don't know what the star is for. You can ignore the four square marks in cells.
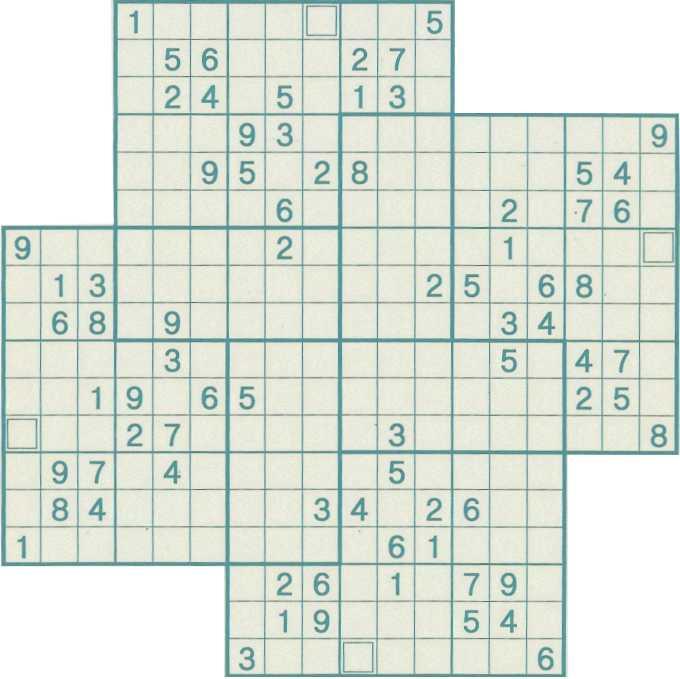
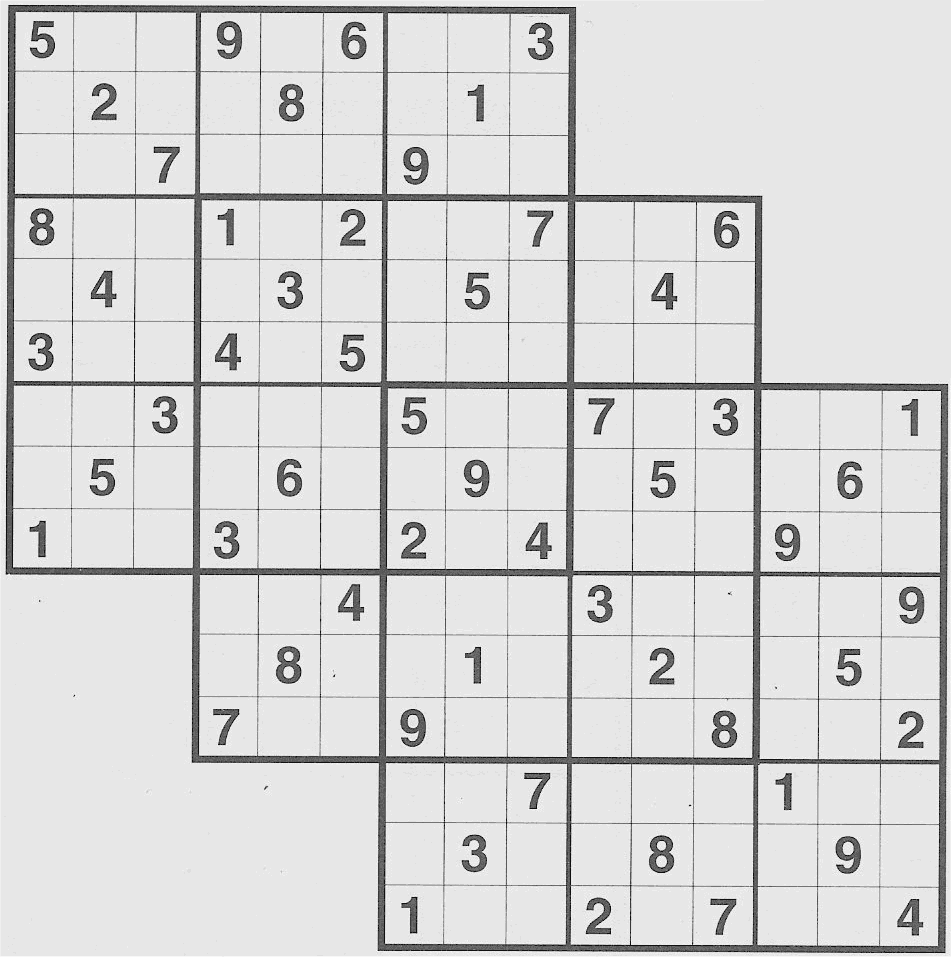
Four overlapping variation
A variation of the standard 4 overlapping puzzle

Five overlapping, standard
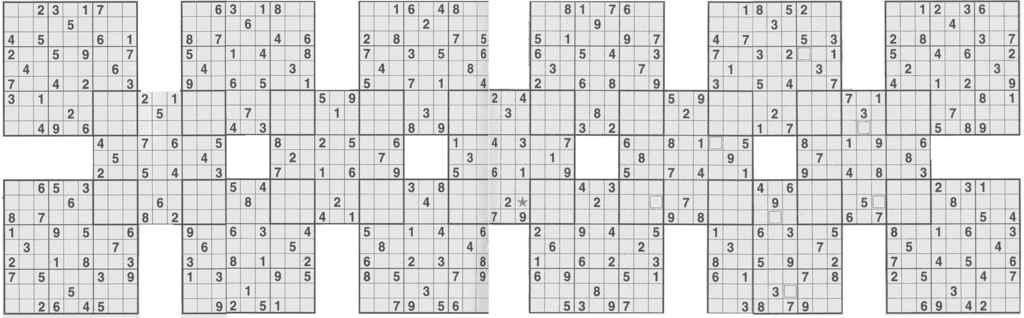
Seventeen overlapping 9x9 puzzles
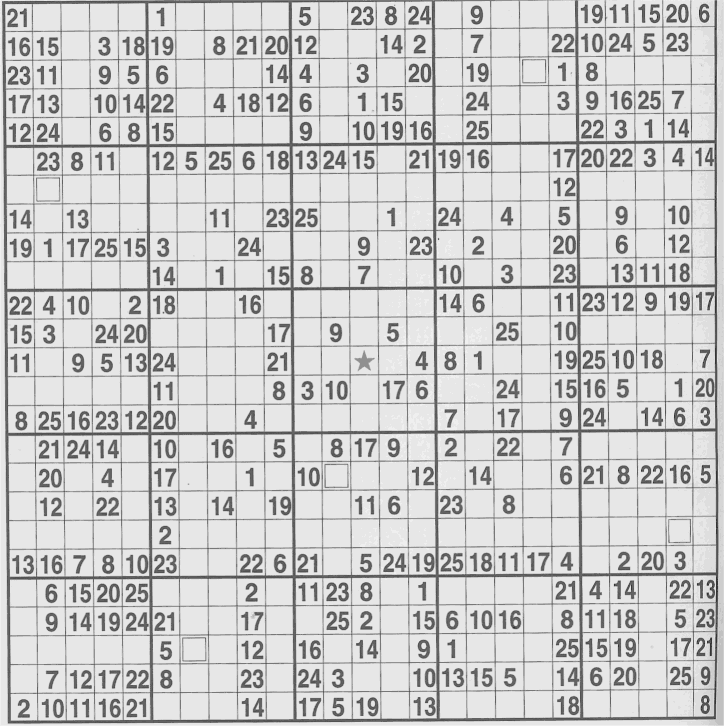
25x25
Notice the English word TEN is embedded in the pattern and it's not quite symmetrcial. |
|
| Back to top |
|
 |
| chuckfresno
| | Joined: 16 Jun 2005 | | Posts: 39 | | : | |
Items |
|
 Posted: Thu Aug 11, 2005 12:37 am Post subject: Posted: Thu Aug 11, 2005 12:37 am Post subject: |
 |
|
Hmm ... looks like I left these three out of the original post:
SUM DOKU

Clues are the sum of several cells. I've also seen these where the PRODUCT is used instead of the SUM.
SEQUENTIAL PUZZLE
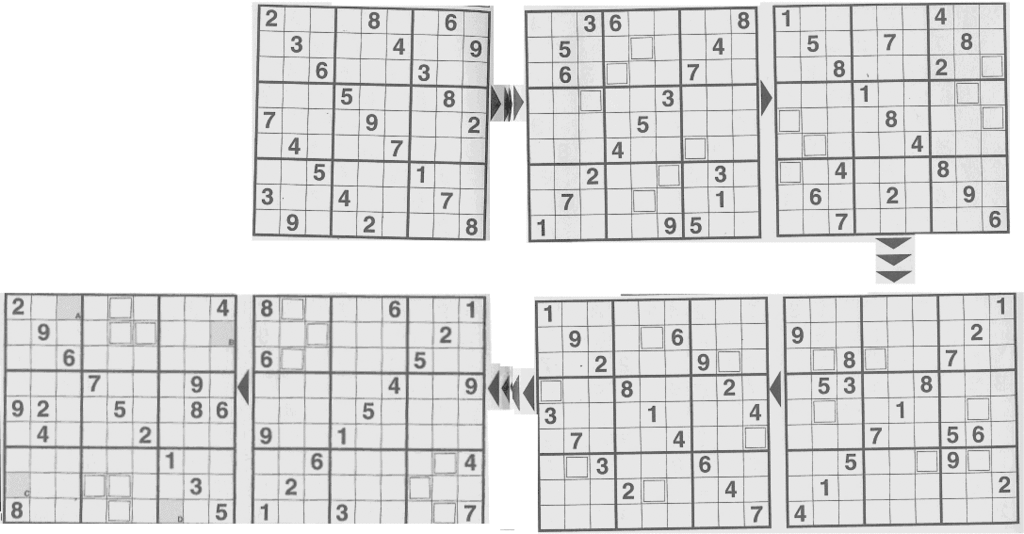
Seqential puzzle.
Must be solved in sequence. Start with upper right, then follow arrows. After solving first puzzle, transfer six numbers in to the cells marked with squares in the second puzzle, etc. Solver may have to work in both directions. Topologicly, this is the same concept as the overlapping puzzles, but in this case, the overlap is disjoint cells. Any cell marked with a square in puzzle X is really one and the same cell in puzzle X-1.
DIAGONALS, NO BOXES
Diagonals, no boxes.
This is a primative variation. Groups are rows, columns and two main diagonals -- no boxes. |
|
| Back to top |
|
 |
| Miles
| | Joined: 29 Dec 2005 | | Posts: 30 | | : | |
Items |
|
 Posted: Thu Dec 29, 2005 5:00 pm Post subject: Posted: Thu Dec 29, 2005 5:00 pm Post subject: |
 |
|
There is anther variant, but I don't have the name, if someone knows.
There are no values in the cases, only indications of comparison between neighboors. |
|
| Back to top |
|
 |
| r3m0t
| | Joined: 16 Feb 2006 | | Posts: 2 | | : | |
Items |
|
 Posted: Thu Feb 16, 2006 12:53 am Post subject: Posted: Thu Feb 16, 2006 12:53 am Post subject: |
 |
|
SUM DOKU is what [i]The Times[i] (UK) calls "Killer Sudoku". It is an area ripe for analysis - I haven't found much material about it on this board.
Creating sum tables was a fascinating programming assignment. I did it in Scheme, and my final version is (imo) beautiful. So for anybody's reference:
1 1 ((1))
2 1 ((2))
3 1 ((3))
3 2 ((2 1))
4 1 ((4))
4 2 ((3 1))
5 1 ((5))
5 2 ((3 2) (4 1))
6 1 ((6))
6 2 ((4 2) (5 1))
6 3 ((3 2 1))
7 1 ((7))
7 2 ((4 3) (5 2) (6 1))
7 3 ((4 2 1))
8 1 ((8))
8 2 ((5 3) (6 2) (7 1))
8 3 ((4 3 1) (5 2 1))
9 1 ((9))
9 2 ((5 4) (6 3) (7 2) (8 1))
9 3 ((4 3 2) (5 3 1) (6 2 1))
10 2 ((6 4) (7 3) (8 2) (9 1))
10 3 ((5 3 2) (5 4 1) (6 3 1) (7 2 1))
10 4 ((4 3 2 1))
11 2 ((6 5) (7 4) (8 3) (9 2))
11 3 ((5 4 2) (6 3 2) (6 4 1) (7 3 1) (8 2 1))
11 4 ((5 3 2 1))
12 2 ((7 5) (8 4) (9 3))
12 3 ((5 4 3) (6 4 2) (6 5 1) (7 3 2) (7 4 1) (8 3 1) (9 2 1))
12 4 ((5 4 2 1) (6 3 2 1))
13 2 ((7 6) (8 5) (9 4))
13 3 ((6 4 3) (6 5 2) (7 4 2) (7 5 1) (8 3 2) (8 4 1) (9 3 1))
13 4 ((5 4 3 1) (6 4 2 1) (7 3 2 1))
14 2 ((8 6) (9 5))
14 3 ((6 5 3) (7 4 3) (7 5 2) (7 6 1) (8 4 2) (8 5 1) (9 3 2) (9 4 1))
14 4 ((5 4 3 2) (6 4 3 1) (6 5 2 1) (7 4 2 1) (8 3 2 1))
15 2 ((8 7) (9 6))
15 3 ((6 5 4) (7 5 3) (7 6 2) (8 4 3) (8 5 2) (8 6 1) (9 4 2) (9 5 1))
15 4 ((6 4 3 2) (6 5 3 1) (7 4 3 1) (7 5 2 1) (8 4 2 1) (9 3 2 1))
15 5 ((5 4 3 2 1))
16 2 ((9 7))
16 3 ((7 5 4) (7 6 3) (8 5 3) (8 6 2) (8 7 1) (9 4 3) (9 5 2) (9 6 1))
16 4 ((6 5 3 2) (6 5 4 1) (7 4 3 2) (7 5 3 1) (7 6 2 1) (8 4 3 1) (8 5 2 1) (9 4 2 1))
16 5 ((6 4 3 2 1))
17 2 ((9 8))
17 3 ((7 6 4) (8 5 4) (8 6 3) (8 7 2) (9 5 3) (9 6 2) (9 7 1))
17 4 ((6 5 4 2) (7 5 3 2) (7 5 4 1) (7 6 3 1) (8 4 3 2) (8 5 3 1) (8 6 2 1) (9 4 3 1) (9 5 2 1))
17 5 ((6 5 3 2 1) (7 4 3 2 1))
18 3 ((7 6 5) (8 6 4) (8 7 3) (9 5 4) (9 6 3) (9 7 2) (9 8 1))
18 4 ((6 5 4 3) (7 5 4 2) (7 6 3 2) (7 6 4 1) (8 5 3 2) (8 5 4 1) (8 6 3 1) (8 7 2 1) (9 4 3 2) (9 5 3 1) (9 6 2 1))
18 5 ((6 5 4 2 1) (7 5 3 2 1) (8 4 3 2 1))
19 3 ((8 6 5) (8 7 4) (9 6 4) (9 7 3) (9 8 2))
19 4 ((7 5 4 3) (7 6 4 2) (7 6 5 1) (8 5 4 2) (8 6 3 2) (8 6 4 1) (8 7 3 1) (9 5 3 2) (9 5 4 1) (9 6 3 1) (9 7 2 1))
19 5 ((6 5 4 3 1) (7 5 4 2 1) (7 6 3 2 1) (8 5 3 2 1) (9 4 3 2 1))
20 3 ((8 7 5) (9 6 5) (9 7 4) (9 8 3))
20 4 ((7 6 4 3) (7 6 5 2) (8 5 4 3) (8 6 4 2) (8 6 5 1) (8 7 3 2) (8 7 4 1) (9 5 4 2) (9 6 3 2) (9 6 4 1) (9 7 3 1) (9 8 2 1))
20 5 ((6 5 4 3 2) (7 5 4 3 1) (7 6 4 2 1) (8 5 4 2 1) (8 6 3 2 1) (9 5 3 2 1))
21 3 ((8 7 6) (9 7 5) (9 8 4))
21 4 ((7 6 5 3) (8 6 4 3) (8 6 5 2) (8 7 4 2) (8 7 5 1) (9 5 4 3) (9 6 4 2) (9 6 5 1) (9 7 3 2) (9 7 4 1) (9 8 3 1))
21 5 ((7 5 4 3 2) (7 6 4 3 1) (7 6 5 2 1) (8 5 4 3 1) (8 6 4 2 1) (8 7 3 2 1) (9 5 4 2 1) (9 6 3 2 1))
21 6 ((6 5 4 3 2 1))
22 3 ((9 7 6) (9 8 5))
22 4 ((7 6 5 4) (8 6 5 3) (8 7 4 3) (8 7 5 2) (8 7 6 1) (9 6 4 3) (9 6 5 2) (9 7 4 2) (9 7 5 1) (9 8 3 2) (9 8 4 1))
22 5 ((7 6 4 3 2) (7 6 5 3 1) (8 5 4 3 2) (8 6 4 3 1) (8 6 5 2 1) (8 7 4 2 1) (9 5 4 3 1) (9 6 4 2 1) (9 7 3 2 1))
22 6 ((7 5 4 3 2 1))
23 3 ((9 8 6))
23 4 ((8 6 5 4) (8 7 5 3) (8 7 6 2) (9 6 5 3) (9 7 4 3) (9 7 5 2) (9 7 6 1) (9 8 4 2) (9 8 5 1))
23 5 ((7 6 5 3 2) (7 6 5 4 1) (8 6 4 3 2) (8 6 5 3 1) (8 7 4 3 1) (8 7 5 2 1) (9 5 4 3 2) (9 6 4 3 1) (9 6 5 2 1) (9 7 4 2 1) (9 8 3 2 1))
23 6 ((7 6 4 3 2 1) (8 5 4 3 2 1))
24 3 ((9 8 7))
24 4 ((8 7 5 4) (8 7 6 3) (9 6 5 4) (9 7 5 3) (9 7 6 2) (9 8 4 3) (9 8 5 2) (9 8 6 1))
24 5 ((7 6 5 4 2) (8 6 5 3 2) (8 6 5 4 1) (8 7 4 3 2) (8 7 5 3 1) (8 7 6 2 1) (9 6 4 3 2) (9 6 5 3 1) (9 7 4 3 1) (9 7 5 2 1) (9 8 4 2 1))
24 6 ((7 6 5 3 2 1) (8 6 4 3 2 1) (9 5 4 3 2 1))
25 4 ((8 7 6 4) (9 7 5 4) (9 7 6 3) (9 8 5 3) (9 8 6 2) (9 8 7 1))
25 5 ((7 6 5 4 3) (8 6 5 4 2) (8 7 5 3 2) (8 7 5 4 1) (8 7 6 3 1) (9 6 5 3 2) (9 6 5 4 1) (9 7 4 3 2) (9 7 5 3 1) (9 7 6 2 1) (9 8 4 3 1) (9 8 5 2 1))
25 6 ((7 6 5 4 2 1) (8 6 5 3 2 1) (8 7 4 3 2 1) (9 6 4 3 2 1))
26 4 ((8 7 6 5) (9 7 6 4) (9 8 5 4) (9 8 6 3) (9 8 7 2))
26 5 ((8 6 5 4 3) (8 7 5 4 2) (8 7 6 3 2) (8 7 6 4 1) (9 6 5 4 2) (9 7 5 3 2) (9 7 5 4 1) (9 7 6 3 1) (9 8 4 3 2) (9 8 5 3 1) (9 8 6 2 1))
26 6 ((7 6 5 4 3 1) (8 6 5 4 2 1) (8 7 5 3 2 1) (9 6 5 3 2 1) (9 7 4 3 2 1))
27 4 ((9 7 6 5) (9 8 6 4) (9 8 7 3))
27 5 ((8 7 5 4 3) (8 7 6 4 2) (8 7 6 5 1) (9 6 5 4 3) (9 7 5 4 2) (9 7 6 3 2) (9 7 6 4 1) (9 8 5 3 2) (9 8 5 4 1) (9 8 6 3 1) (9 8 7 2 1))
27 6 ((7 6 5 4 3 2) (8 6 5 4 3 1) (8 7 5 4 2 1) (8 7 6 3 2 1) (9 6 5 4 2 1) (9 7 5 3 2 1) (9 8 4 3 2 1))
28 4 ((9 8 6 5) (9 8 7 4))
28 5 ((8 7 6 4 3) (8 7 6 5 2) (9 7 5 4 3) (9 7 6 4 2) (9 7 6 5 1) (9 8 5 4 2) (9 8 6 3 2) (9 8 6 4 1) (9 8 7 3 1))
28 6 ((8 6 5 4 3 2) (8 7 5 4 3 1) (8 7 6 4 2 1) (9 6 5 4 3 1) (9 7 5 4 2 1) (9 7 6 3 2 1) (9 8 5 3 2 1))
28 7 ((7 6 5 4 3 2 1))
29 4 ((9 8 7 5))
29 5 ((8 7 6 5 3) (9 7 6 4 3) (9 7 6 5 2) (9 8 5 4 3) (9 8 6 4 2) (9 8 6 5 1) (9 8 7 3 2) (9 8 7 4 1))
29 6 ((8 7 5 4 3 2) (8 7 6 4 3 1) (8 7 6 5 2 1) (9 6 5 4 3 2) (9 7 5 4 3 1) (9 7 6 4 2 1) (9 8 5 4 2 1) (9 8 6 3 2 1))
29 7 ((8 6 5 4 3 2 1))
30 4 ((9 8 7 6))
30 5 ((8 7 6 5 4) (9 7 6 5 3) (9 8 6 4 3) (9 8 6 5 2) (9 8 7 4 2) (9 8 7 5 1))
30 6 ((8 7 6 4 3 2) (8 7 6 5 3 1) (9 7 5 4 3 2) (9 7 6 4 3 1) (9 7 6 5 2 1) (9 8 5 4 3 1) (9 8 6 4 2 1) (9 8 7 3 2 1))
30 7 ((8 7 5 4 3 2 1) (9 6 5 4 3 2 1))
31 5 ((9 7 6 5 4) (9 8 6 5 3) (9 8 7 4 3) (9 8 7 5 2) (9 8 7 6 1))
31 6 ((8 7 6 5 3 2) (8 7 6 5 4 1) (9 7 6 4 3 2) (9 7 6 5 3 1) (9 8 5 4 3 2) (9 8 6 4 3 1) (9 8 6 5 2 1) (9 8 7 4 2 1))
31 7 ((8 7 6 4 3 2 1) (9 7 5 4 3 2 1))
32 5 ((9 8 6 5 4) (9 8 7 5 3) (9 8 7 6 2))
32 6 ((8 7 6 5 4 2) (9 7 6 5 3 2) (9 7 6 5 4 1) (9 8 6 4 3 2) (9 8 6 5 3 1) (9 8 7 4 3 1) (9 8 7 5 2 1))
32 7 ((8 7 6 5 3 2 1) (9 7 6 4 3 2 1) (9 8 5 4 3 2 1))
33 5 ((9 8 7 5 4) (9 8 7 6 3))
33 6 ((8 7 6 5 4 3) (9 7 6 5 4 2) (9 8 6 5 3 2) (9 8 6 5 4 1) (9 8 7 4 3 2) (9 8 7 5 3 1) (9 8 7 6 2 1))
33 7 ((8 7 6 5 4 2 1) (9 7 6 5 3 2 1) (9 8 6 4 3 2 1))
34 5 ((9 8 7 6 4))
34 6 ((9 7 6 5 4 3) (9 8 6 5 4 2) (9 8 7 5 3 2) (9 8 7 5 4 1) (9 8 7 6 3 1))
34 7 ((8 7 6 5 4 3 1) (9 7 6 5 4 2 1) (9 8 6 5 3 2 1) (9 8 7 4 3 2 1))
35 5 ((9 8 7 6 5))
35 6 ((9 8 6 5 4 3) (9 8 7 5 4 2) (9 8 7 6 3 2) (9 8 7 6 4 1))
35 7 ((8 7 6 5 4 3 2) (9 7 6 5 4 3 1) (9 8 6 5 4 2 1) (9 8 7 5 3 2 1))
36 6 ((9 8 7 5 4 3) (9 8 7 6 4 2) (9 8 7 6 5 1))
36 7 ((9 7 6 5 4 3 2) (9 8 6 5 4 3 1) (9 8 7 5 4 2 1) (9 8 7 6 3 2 1))
36 8 ((8 7 6 5 4 3 2 1))
37 6 ((9 8 7 6 4 3) (9 8 7 6 5 2))
37 7 ((9 8 6 5 4 3 2) (9 8 7 5 4 3 1) (9 8 7 6 4 2 1))
37 8 ((9 7 6 5 4 3 2 1))
38 6 ((9 8 7 6 5 3))
38 7 ((9 8 7 5 4 3 2) (9 8 7 6 4 3 1) (9 8 7 6 5 2 1))
38 8 ((9 8 6 5 4 3 2 1))
39 6 ((9 8 7 6 5 4))
39 7 ((9 8 7 6 4 3 2) (9 8 7 6 5 3 1))
39 8 ((9 8 7 5 4 3 2 1))
40 7 ((9 8 7 6 5 3 2) (9 8 7 6 5 4 1))
40 8 ((9 8 7 6 4 3 2 1))
41 7 ((9 8 7 6 5 4 2))
41 8 ((9 8 7 6 5 3 2 1))
42 7 ((9 8 7 6 5 4 3))
42 8 ((9 8 7 6 5 4 2 1))
43 8 ((9 8 7 6 5 4 3 1))
44 8 ((9 8 7 6 5 4 3 2))
45 9 ((9 8 7 6 5 4 3 2 1))
PS The above post should mention that dotted groups may not contain the same number twice - even if they are not in the same row, column, and 3x3 block. |
|
| Back to top |
|
 |
| aman
| | Joined: 19 Nov 2006 | | Posts: 43 | | : | | Location: Singapore |
Items |
|
 Posted: Sun Nov 19, 2006 11:27 am Post subject: Posted: Sun Nov 19, 2006 11:27 am Post subject: |
 |
|
It is a pity that there is no communication between the Japanese and the rest of the world with regard to Sudoku.
Hence, nothing is known about the original inventors of many Sudoku variants. Can any Japanese publisher, editor, writer or "Sudokuist" who happens to visit this forum provide any information about the original inventors of the above variants? |
|
| Back to top |
|
 |
| aman
| | Joined: 19 Nov 2006 | | Posts: 43 | | : | | Location: Singapore |
Items |
|
 Posted: Sun Nov 19, 2006 11:32 am Post subject: Posted: Sun Nov 19, 2006 11:32 am Post subject: |
 |
|
| Miles, you should post the image of the Sudoku variant even if you don't know its name. I am sure many people would like to take a look at it. |
|
| Back to top |
|
 |
|
|
You cannot post new topics in this forum
You cannot reply to topics in this forum
You cannot edit your posts in this forum
You cannot delete your posts in this forum
You cannot vote in polls in this forum
|

Powered by phpBB © 2001, 2005 phpBB Group
Igloo Theme Version 1.0 :: Created By: Andrew Charron |




















