
|
| View previous topic :: View next topic |
| Author |
Message |
| dobrichev
| | Joined: 18 Dec 2009 | | Posts: 28 | | : | |
Items |
|
 Posted: Thu Feb 25, 2010 2:30 pm Post subject: Solution Grids in U-Space (Unavoidable Sets) Posted: Thu Feb 25, 2010 2:30 pm Post subject: Solution Grids in U-Space (Unavoidable Sets) |
 |
|
Unavoidable Set is a subset of cells in the Sudoku grid, where at least one clue must be given in order the puzzle to have unique solution. It has been discussed in details in the forums years ago.
The smallest Unavoidable Set I can imagine is of size 4. It is a symmetry in 4 cells located in 2 boxes and forming a rectangle where the diagonal digits are the same. Such symmetries are easy and fast to be found in a known complete grid.
Performing the counting of the size 4 sets on the whole set of the essentially different sudoku grids resulted in the following:
EDIT: There was a bug and the data have been recalculated and updated after the fix.
| Code: | #sets GridCount
0 352894
1 1654475
2 6891532
3 21107315
4 51765007
5 105759561
6 186644998
7 289799298
8 402555715
9 505627121
10 580153348
11 612280600
12 598177291
13 543232929
14 460415833
15 364777309
16 270755777
17 188260086
18 122672303
19 74788269
20 42628010
21 22634443
22 11177578
23 5123654
24 2176664
25 854253
26 311585
27 105410
28 33612
29 9897
30 2798
31 721
32 186
33 43
34 14
35 0
36 9 |
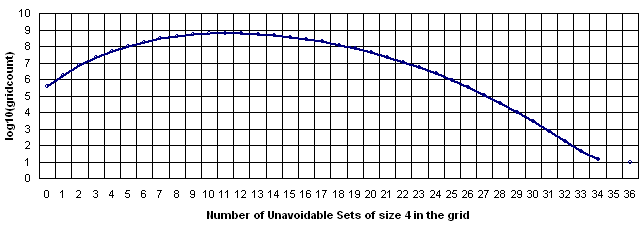
The whole set of the essentially different sudoku grids has been generated by Glenn Fowler's tool (which does almost everything, and the generation as he said took about 1 week). Later each grid has been compressed in 10 bytes format resulting in 54 GB file.
The counting pass took about 8 hours on 2.8GHz machine.
Here is the counting code:
EDIT: Initial version of the lookup table was buggy. Updated with the (hopefully) correct one.
[code size=1]static const int gr4unav[81][6][3] =
{
{{12, 3, 9},{13, 4, 9},{14, 5, 9},{28, 1,27},{37, 1,36},{46, 1,45}},
{{12, 3,10},{13, 4,10},{14, 5,10},{29, 2,28},{38, 2,37},{47, 2,46}},
{{12, 3,11},{13, 4,11},{14, 5,11},{27, 0,29},{36, 0,38},{45, 0,47}},
{{15, 6,12},{16, 7,12},{17, 8,12},{31, 4,30},{40, 4,39},{49, 4,48}},
{{15, 6,13},{16, 7,13},{17, 8,13},{32, 5,31},{41, 5,40},{50, 5,49}},
{{15, 6,14},{16, 7,14},{17, 8,14},{30, 3,32},{39, 3,41},{48, 3,50}},
{{ 9, 0,15},{10, 1,15},{11, 2,15},{34, 7,33},{43, 7,42},{52, 7,51}},
{{ 9, 0,16},{10, 1,16},{11, 2,16},{35, 8,34},{44, 8,43},{53, 8,52}},
{{ 9, 0,17},{10, 1,17},{11, 2,17},{33, 6,35},{42, 6,44},{51, 6,53}},
{{21,12,18},{22,13,18},{23,14,18},{28,10,27},{37,10,36},{46,10,45}},
{{21,12,19},{22,13,19},{23,14,19},{29,11,28},{38,11,37},{47,11,46}},
{{21,12,20},{22,13,20},{23,14,20},{27, 9,29},{36, 9,38},{45, 9,47}},
{{24,15,21},{25,16,21},{26,17,21},{31,13,30},{40,13,39},{49,13,48}},
{{24,15,22},{25,16,22},{26,17,22},{32,14,31},{41,14,40},{50,14,49}},
{{24,15,23},{25,16,23},{26,17,23},{30,12,32},{39,12,41},{48,12,50}},
{{18, 9,24},{19,10,24},{20,11,24},{34,16,33},{43,16,42},{52,16,51}},
{{18, 9,25},{19,10,25},{20,11,25},{35,17,34},{44,17,43},{53,17,52}},
{{18, 9,26},{19,10,26},{20,11,26},{33,15,35},{42,15,44},{51,15,53}},
{{ 3, 0,21},{ 4, 0,22},{ 5, 0,23},{28,19,27},{37,19,36},{46,19,45}},
{{ 3, 1,21},{ 4, 1,22},{ 5, 1,23},{29,20,28},{38,20,37},{47,20,46}},
{{ 3, 2,21},{ 4, 2,22},{ 5, 2,23},{27,18,29},{36,18,38},{45,18,47}},
{{ 6, 3,24},{ 7, 3,25},{ 8, 3,26},{31,22,30},{40,22,39},{49,22,48}},
{{ 6, 4,24},{ 7, 4,25},{ 8, 4,26},{32,23,31},{41,23,40},{50,23,49}},
{{ 6, 5,24},{ 7, 5,25},{ 8, 5,26},{30,21,32},{39,21,41},{48,21,50}},
{{ 0, 6,18},{ 1, 6,19},{ 2, 6,20},{34,25,33},{43,25,42},{52,25,51}},
{{ 0, 7,18},{ 1, 7,19},{ 2, 7,20},{35,26,34},{44,26,43},{53,26,52}},
{{ 0, 8,18},{ 1, 8,19},{ 2, 8,20},{33,24,35},{42,24,44},{51,24,53}},
{{39,30,36},{40,31,36},{41,32,36},{55,28,54},{64,28,63},{73,28,72}},
{{39,30,37},{40,31,37},{41,32,37},{56,29,55},{65,29,64},{74,29,73}},
{{39,30,38},{40,31,38},{41,32,38},{54,27,56},{63,27,65},{72,27,74}},
{{42,33,39},{43,34,39},{44,35,39},{58,31,57},{67,31,66},{76,31,75}},
{{42,33,40},{43,34,40},{44,35,40},{59,32,58},{68,32,67},{77,32,76}},
{{42,33,41},{43,34,41},{44,35,41},{57,30,59},{66,30,68},{75,30,77}},
{{36,27,42},{37,28,42},{38,29,42},{61,34,60},{70,34,69},{79,34,78}},
{{36,27,43},{37,28,43},{38,29,43},{62,35,61},{71,35,70},{80,35,79}},
{{36,27,44},{37,28,44},{38,29,44},{60,33,62},{69,33,71},{78,33,80}},
{{48,39,45},{49,40,45},{50,41,45},{55,37,54},{64,37,63},{73,37,72}},
{{48,39,46},{49,40,46},{50,41,46},{56,38,55},{65,38,64},{74,38,73}},
{{48,39,47},{49,40,47},{50,41,47},{54,36,56},{63,36,65},{72,36,74}},
{{51,42,48},{52,43,48},{53,44,48},{58,40,57},{67,40,66},{76,40,75}},
{{51,42,49},{52,43,49},{53,44,49},{59,41,58},{68,41,67},{77,41,76}},
{{51,42,50},{52,43,50},{53,44,50},{57,39,59},{66,39,68},{75,39,77}},
{{45,36,51},{46,37,51},{47,38,51},{61,43,60},{70,43,69},{79,43,78}},
{{45,36,52},{46,37,52},{47,38,52},{62,44,61},{71,44,70},{80,44,79}},
{{45,36,53},{46,37,53},{47,38,53},{60,42,62},{69,42,71},{78,42,80}},
{{30,27,48},{31,27,49},{32,27,50},{55,46,54},{64,46,63},{73,46,72}},
{{30,28,48},{31,28,49},{32,28,50},{56,47,55},{65,47,64},{74,47,73}},
{{30,29,48},{31,29,49},{32,29,50},{54,45,56},{63,45,65},{72,45,74}},
{{33,30,51},{34,30,52},{35,30,53},{58,49,57},{67,49,66},{76,49,75}},
{{33,31,51},{34,31,52},{35,31,53},{59,50,58},{68,50,67},{77,50,76}},
{{33,32,51},{34,32,52},{35,32,53},{57,48,59},{66,48,68},{75,48,77}},
{{27,33,45},{28,33,46},{29,33,47},{61,52,60},{70,52,69},{79,52,78}},
{{27,34,45},{28,34,46},{29,34,47},{62,53,61},{71,53,70},{80,53,79}},
{{27,35,45},{28,35,46},{29,35,47},{60,51,62},{69,51,71},{78,51,80}},
{{66,57,63},{67,58,63},{68,59,63},{ 1, 0,55},{10, 9,55},{19,18,55}},
{{66,57,64},{67,58,64},{68,59,64},{ 2, 1,56},{11,10,56},{20,19,56}},
{{66,57,65},{67,58,65},{68,59,65},{ 0, 2,54},{ 9,11,54},{18,20,54}},
{{69,60,66},{70,61,66},{71,62,66},{ 4, 3,58},{13,12,58},{22,21,58}},
{{69,60,67},{70,61,67},{71,62,67},{ 5, 4,59},{14,13,59},{23,22,59}},
{{69,60,68},{70,61,68},{71,62,68},{ 3, 5,57},{12,14,57},{21,23,57}},
{{63,54,69},{64,55,69},{65,56,69},{ 7, 6,61},{16,15,61},{25,24,61}},
{{63,54,70},{64,55,70},{65,56,70},{ 8, 7,62},{17,16,62},{26,25,62}},
{{63,54,71},{64,55,71},{65,56,71},{ 6, 8,60},{15,17,60},{24,26,60}},
{{75,66,72},{76,67,72},{77,68,72},{ 1, 0,64},{10, 9,64},{19,18,64}},
{{75,66,73},{76,67,73},{77,68,73},{ 2, 1,65},{11,10,65},{20,19,65}},
{{75,66,74},{76,67,74},{77,68,74},{ 0, 2,63},{ 9,11,63},{18,20,63}},
{{78,69,75},{79,70,75},{80,71,75},{ 4, 3,67},{13,12,67},{22,21,67}},
{{78,69,76},{79,70,76},{80,71,76},{ 5, 4,68},{14,13,68},{23,22,68}},
{{78,69,77},{79,70,77},{80,71,77},{ 3, 5,66},{12,14,66},{21,23,66}},
{{72,63,78},{73,64,78},{74,65,78},{ 7, 6,70},{16,15,70},{25,24,70}},
{{72,63,79},{73,64,79},{74,65,79},{ 8, 7,71},{17,16,71},{26,25,71}},
{{72,63,80},{73,64,80},{74,65,80},{ 6, 8,69},{15,17,69},{24,26,69}},
{{57,54,75},{58,54,76},{59,54,77},{ 1, 0,73},{10, 9,73},{19,18,73}},
{{57,55,75},{58,55,76},{59,55,77},{ 2, 1,74},{11,10,74},{20,19,74}},
{{57,56,75},{58,56,76},{59,56,77},{ 0, 2,72},{ 9,11,72},{18,20,72}},
{{60,57,78},{61,57,79},{62,57,80},{ 4, 3,76},{13,12,76},{22,21,76}},
{{60,58,78},{61,58,79},{62,58,80},{ 5, 4,77},{14,13,77},{23,22,77}},
{{60,59,78},{61,59,79},{62,59,80},{ 3, 5,75},{12,14,75},{21,23,75}},
{{54,60,72},{55,60,73},{56,60,74},{ 7, 6,79},{16,15,79},{25,24,79}},
{{54,61,72},{55,61,73},{56,61,74},{ 8, 7,80},{17,16,80},{26,25,80}},
{{54,62,72},{55,62,73},{56,62,74},{ 6, 8,78},{15,17,78},{24,26,78}}
};
extern int unav4(char *g) {
int i, j, n = 0;
for(i = 0; i < 81; i++) {
for(j = 0; j < 3; j++) {
if(g[i] == g[gr4unav[i][j][0]]) {
if(g[gr4unav[i][j][1]] == g[gr4unav[i][j][2]]) {
n++;
}
break;
}
}
for(j = 3; j < 6; j++) {
if(g[i] == g[gr4unav[i][j][0]]) {
if(g[gr4unav[i][j][1]] == g[gr4unav[i][j][2]]) {
n++;
}
break;
}
}
}
return n;
}[/code]
The compression/decompression code as well as the 54GB data file may be published too. Please PM me if interested.
The results are not double checked so there may be some stupid errors. Especially in the lookup table which is hand-made.
I have still no idea wheter this information is useful. At least we have one more column in the whole grid table (along with the grid itself and the authomorphism level).
Enjoy!
EDIT: March/9/2010 Changed subject from "Unavoidable Sets of size 4".
Mladen Dobrichev
Last edited by dobrichev on Tue Mar 09, 2010 7:21 pm; edited 4 times in total |
|
| Back to top |
|
 |
| JPF
| | Joined: 05 Dec 2005 | | Posts: 29 | | : | | Location: Paris |
Items |
|
 Posted: Thu Feb 25, 2010 8:04 pm Post subject: Posted: Thu Feb 25, 2010 8:04 pm Post subject: |
 |
|
Interesting, thanks.
Here Red Ed claimed 9 grids, up to isomorphism, with 36 U4s.
JPF |
|
| Back to top |
|
 |
| dobrichev
| | Joined: 18 Dec 2009 | | Posts: 28 | | : | |
Items |
|
 Posted: Fri Feb 26, 2010 6:49 pm Post subject: Posted: Fri Feb 26, 2010 6:49 pm Post subject: |
 |
|
Thank you for the link!
The data have been recalculated and the table and picture are updated.
The pass took 14088 seconds (~4 hours) for the 5472730538 grids on 2x2.8GHz Pentium D. It is ~2.57 us/grid or ~70 000 grids per core per GHz. |
|
| Back to top |
|
 |
| JPF
| | Joined: 05 Dec 2005 | | Posts: 29 | | : | | Location: Paris |
Items |
|
 Posted: Fri Feb 26, 2010 10:40 pm Post subject: Posted: Fri Feb 26, 2010 10:40 pm Post subject: |
 |
|
I don't want to pit nick, but here
| Red Ed wrote: | | JPF wrote: | | Red Ed wrote: | | Back to size-4 unavoidables: the average number is exactly 320784513273 / 27704267971, or roughly 11.58 per grid. |
Excellent , but where are these numbers coming from ? |
Let p(X,g) be the probability of finding X in a particular (fixed) position within a band represented by "gangster" g. These aren't too hard to work out. Then p(X), the probability of finding X in a particular position in any grid, is just the average of these, weighting p(X,g) proportional to the number of extensions of gangster g to a full grid (i.e. not quite uniformly). You'll recognise the denominator, 27704267971, as the big prime in the 6.67e21 number. Finally, E(X) = 486 * p(X). |
There is still a slight difference between Red Ed's average number and yours (63 367 542 018 / 5 472 730 538)
Who's right?
A matter of precision in Red Ed's calculation?
JPF |
|
| Back to top |
|
 |
| dobrichev
| | Joined: 18 Dec 2009 | | Posts: 28 | | : | |
Items |
|
 Posted: Sat Feb 27, 2010 12:30 am Post subject: Posted: Sat Feb 27, 2010 12:30 am Post subject: |
 |
|
The data posted here represents the essentially different grids.
Since Red Ed uses this average to check the bias of the grid generators he should use all valid grids as a basis. The difference between the number of the essentially different grids scaled by the number of permutations, from one side, and the number of all valid grids, from other side, is in the automorphism. The grids with automorphism must be scaled by a factor less than the whole number of permutations.
While recompressing the grids I lost the authomorphism data - the algorithm I am using fits in 79 bits and I decided to omit the authomorphism level generated by gsf's tool. So I can't take into account the count of unavailable sets of size 4 for each of the grids with authomorphism.
In the counting algorithm only integers are used so there can't be lost of precision. Hope it is true for RedEd's calculations too. Excluding the bugs, the data which are out of my control is the list of the grids but I don't intend to verify the generator.
If I am right, the conclusion is that the subset of all the grids with authomorphism is biased using the number of U4 sets as criterion. This is expected 1) as effect of their statistically unrepresentative number, and 2) due to the degree of internal symmetry the both indicators are measuring for.  |
|
| Back to top |
|
 |
| JPF
| | Joined: 05 Dec 2005 | | Posts: 29 | | : | | Location: Paris |
Items |
|
 Posted: Sat Feb 27, 2010 9:32 pm Post subject: Posted: Sat Feb 27, 2010 9:32 pm Post subject: |
 |
|
Good points dobrichev 
Here are the numbers for all the sudokus :
| Code: |
#sets GridCount
0 417919339935498240
1 2016801894998016000
2 8386580817836605440
3 25727729542848184320
4 63071690010443735040
5 128917929120139837440
6 227475661815015505920
7 353261364528421601280
8 490662706800117841920
9 616354232496294297600
10 707153569110802759680
11 746365938211655516160
12 729132320509634764800
13 662197715497125642240
14 561214465571146383360
15 444660909332040253440
16 330030904476986818560
17 229487990799621980160
18 149525322190616494080
19 91166445141047377920
20 51957643438158151680
21 27591045963883315200
22 13622702775818895360
23 6245687962923171840
24 2651975487232081920
25 1041326695899463680
26 379339411779256320
27 128471565061324800
28 40798647682007040
29 12064424276459520
30 3341883313520640
31 878897635983360
32 210277173657600
33 49978922434560
34 15237476352000
35 0
36 2167107747840
total 6670903752021072936960
|
Red Ed's ratio is therefore:
77241622677889068564480 / 6670903752021072936960 = 11.5788842935242917990
JPF |
|
| Back to top |
|
 |
| dobrichev
| | Joined: 18 Dec 2009 | | Posts: 28 | | : | |
Items |
|
 Posted: Sun Feb 28, 2010 11:37 pm Post subject: Posted: Sun Feb 28, 2010 11:37 pm Post subject: |
 |
|
Wow! It is a very good result.
It seems there are no grids with authomorphism having 1, 29, and 31 U4.
Did you apply scaling and corrections for U4s for the 560151 grids with authomorphism over the table on the top (the U4s int the essentially different grids) or use some different method?
BTW it gives me pleasure this time you didn't respond with a link to article dated 2006  |
|
| Back to top |
|
 |
| JPF
| | Joined: 05 Dec 2005 | | Posts: 29 | | : | | Location: Paris |
Items |
|
 Posted: Mon Mar 01, 2010 9:55 am Post subject: Posted: Mon Mar 01, 2010 9:55 am Post subject: |
 |
|
| dobrichev wrote: | | Did you apply scaling and corrections for U4s for the 560151 grids with authomorphism over the table on the top (the U4s int the essentially different grids |
Yes, it's exactly what i did.
The calculation of Red Ed's ratio (average number of U4 on all the sudokus) is an indirect way of checking your table.
Red Ed gave : A1 = 320784513273 / 27704267971
I got : A2 = 77241622677889068564480 / 6670903752021072936960
As we now :
6670903752021072936960 = 9! x (72^2) x (2^7) x 27704267971 = 240789749760 x 27704267971
And it appears that :
77241622677889068564480 = 240789749760 x 320784513273
The numbers A1 and A2 are exactly the same.
| dobrichev wrote: | | It seems there are no grids with authomorphism having 1, 29, and 31 U4. |
Yes, and no 35 as well. Here are the data :
| Code: |
#U4 automorphic grids
0 18671
2 23133
3 3150
4 48584
5 4554
6 71825
7 5630
8 85015
9 6597
10 85680
11 4848
12 72679
13 3605
14 51738
15 2926
16 32544
17 1145
18 19393
19 514
20 9523
21 412
22 4495
23 60
24 2178
25 10
26 790
27 28
28 281
30 103
32 25
33 3
34 3
36 9
total 560151
|
JPF |
|
| Back to top |
|
 |
| dobrichev
| | Joined: 18 Dec 2009 | | Posts: 28 | | : | |
Items |
|
 Posted: Tue Mar 02, 2010 1:19 pm Post subject: Posted: Tue Mar 02, 2010 1:19 pm Post subject: |
 |
|
Fine!
Altrough I'm not sure the result is truly independent, it is a confirmation of the Red Ed's calculations.
In the next days I'll try to see could the U6 be found in a reasonable processing time, and then eventyally make a matrix of 36x? with the grid count of U4 and U6.
Later a MCN calculation could be tried, taking into account only U4 and U6. Have no idea about the processing time. |
|
| Back to top |
|
 |
| dobrichev
| | Joined: 18 Dec 2009 | | Posts: 28 | | : | |
Items |
|
 Posted: Tue Mar 09, 2010 6:53 am Post subject: Grids in U6/U4 Space Posted: Tue Mar 09, 2010 6:53 am Post subject: Grids in U6/U4 Space |
 |
|
Hello again,
There are some results for Unavoidable Sets of size 6 (U6) available.
Surprisingly for me, processing of U6 can be done fast too. A pass trough entire set of 5 472 730 538 grids took about 1 kWh (6 hours on 2 core Pentium 2.8).
All the results below are based on the raw data for All 5472730538 Grids, Solutions of 48826 17-clue Puzzles, and 53 Grids of the known 39-clue Puzzles.
The known noice in the data is:
- The set of the all Essentially Different Grids is not representative for counting w/o taking into account the authomorphism. It is not taken into account. The portion of the authomorphic grids is about 0.00005073. - The set of the 17-clue puzzles includes a duplicate of the grid for each representative puzzle. - Count axis in the pictures is in logarithmic scale. Linear is not representative. The formula used is log10(1 + count) avoiding the uncertainity for the values of zero.
Counting U6
There are 4 types of U6 I found in the source code of Sudoku Checker.
| Code: | type 1 type 2 type 3 type 4
=====================================================
AB* *** *** AB* *** *** ABC *** *** AB* *** ***
*** *** *** *** *** *** *** *** *** *** *** ***
*** *** *** *** *** *** *** *** *** *** *** ***
BC* *** *** B*A *** *** BCA *** *** B** A** ***
*** *** *** *** *** *** *** *** *** *A* B** ***
*** *** *** *** *** *** *** *** *** *** *** ***
CA* *** *** *AB *** *** *** *** *** *** *** ***
*** *** *** *** *** *** *** *** *** *** *** ***
*** *** *** *** *** *** *** *** *** *** *** *** |
The process counts the grids of each type separately, but no correlations between different types of U6 in the same grid have been searched yet.
Here is the distribution of the grids by the U6 types. The total for each type is the total of the gridset.
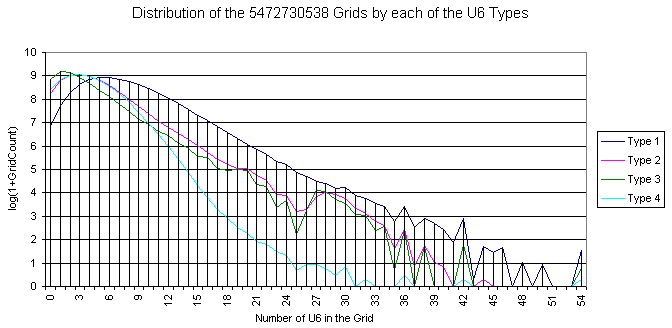
For each of the types there are some harmonics with period of 4 and 6. (Maybe with 2, 7, and 9 too). In general for the small values the curve is not smooth.
Similarly, the curve for the grid count per all types of U6 is ugly.
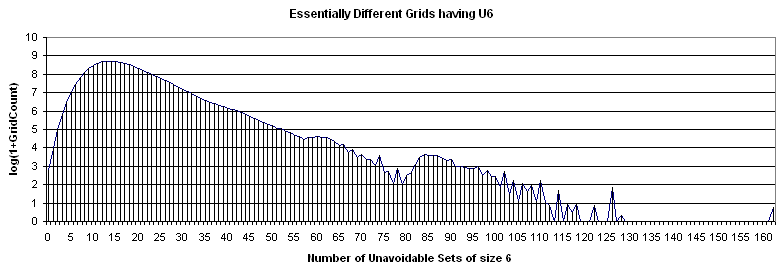
Some additional statistics
| Code: | *MC grid has 54+54+54+0 U6
*SF grid has 9+1+1+3 U6
Totals by U6 Type (Sum(#Grids * #UA)
====================================
Type 1 35322092372 42%
Type 2 18942666506 23%
Type 3 11863428613 14%
Type 4 17843252067 21%
---------------------
Total 83971439558
Average T1/Grid = 6.45
Average T2/Grid = 3.46
Average T3/Grid = 2.17
Average T4/Grid = 3.26
Average U6/Grid = 15.34
|
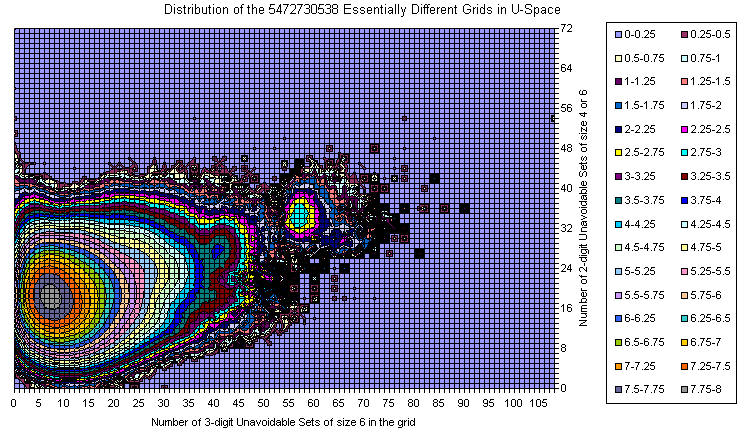
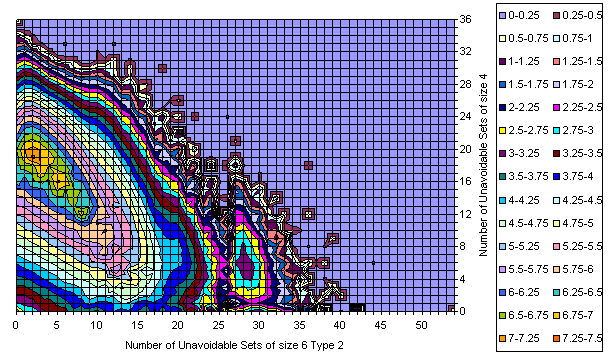
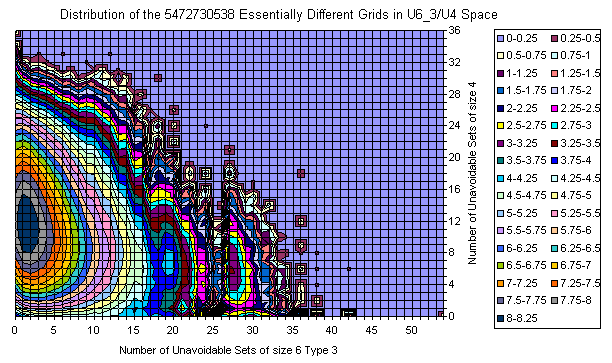
Sudoku Grids in U4/U6 Space
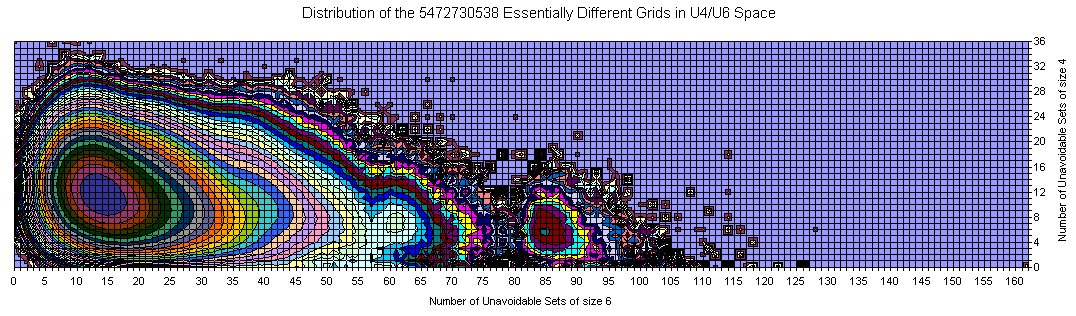
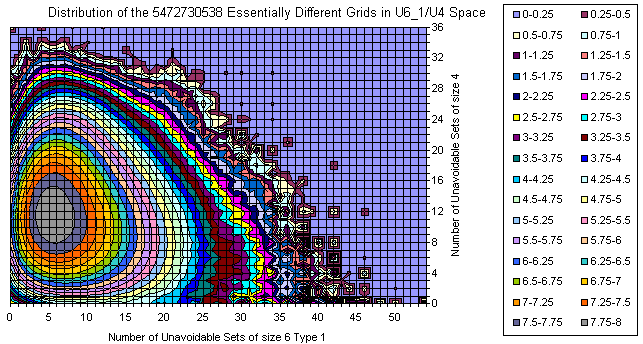
The majority of the grids is covered with a smooth manifold having bright maximum. With increase of the U6 and slightly decrease of U4 there are two smaller peaks.
The extremes are 192 U6 with 0 U4 (one of them is the Most Canonical Grid) and several 36 U4 located close to the main peak in the U6 direction.
There are lots of islands which are attractive on the picture but with few representative grids.
There is an empty space near (0,0) but as a whole there are lots of grids resided on one of the zero axes.
There are no islands in the upper right corner.
There is correlation between U4 and U6.
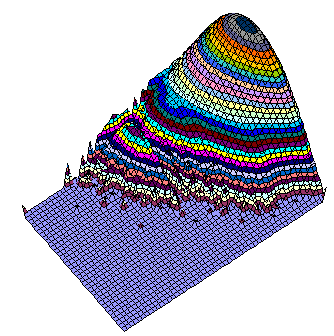
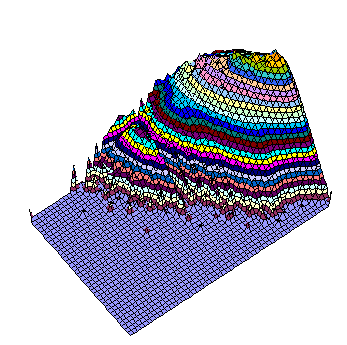
The amount of the grids out of the main peak is visible from the 3D views below (same data, different Z scale, but logarithmic everywhere).
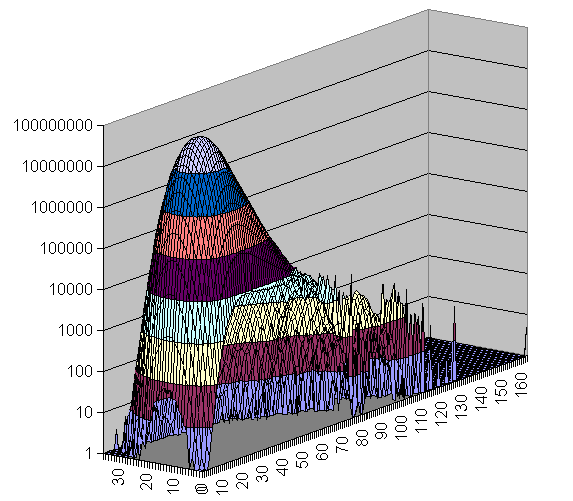 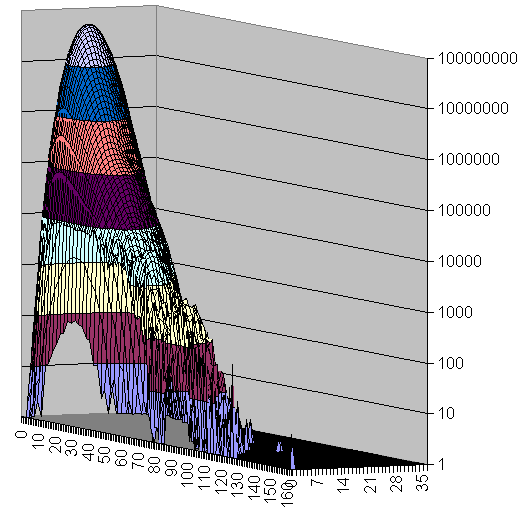
There is well visible trend the number of U4 to decrease with increasing of U6.
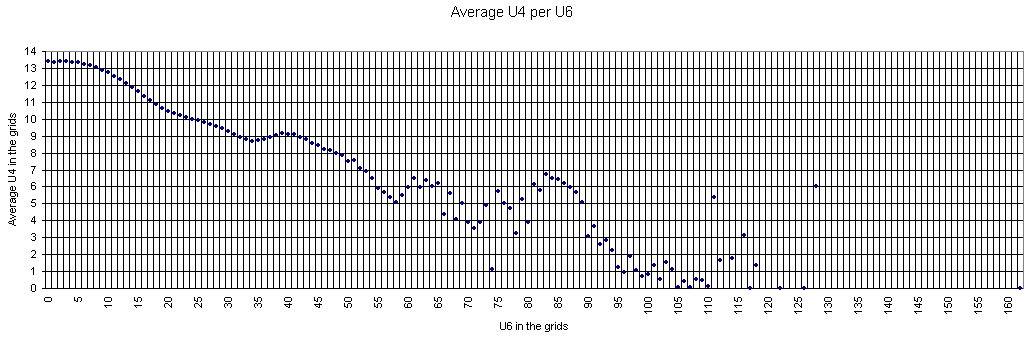
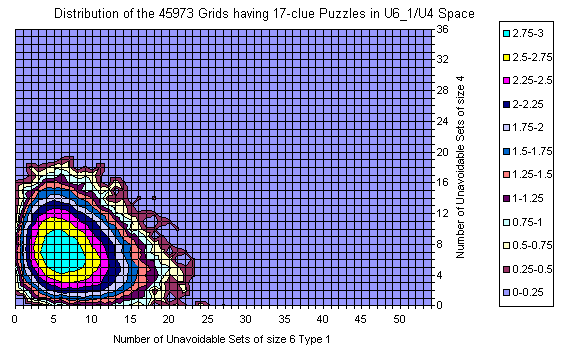
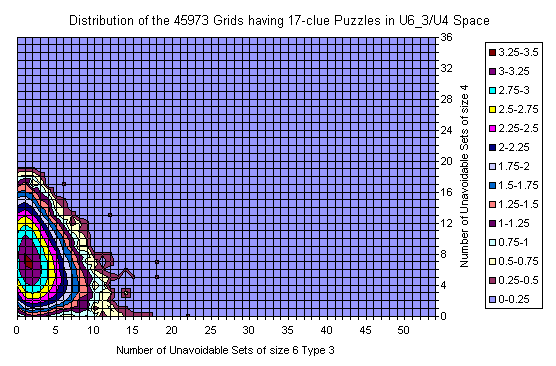
Grids of the 17-clue and 39-clue Puzzles
Here is the data for the 17-clue puzzles. As mentioned above the data is not 1:1 comparable since in 17-clue set each puzzle is represented with its own copy of the grid and there are duplicate grids (weighted by # of puzzles). Basis is the Gordon Royle's set with 48826 puzzles. For 39-clues the set consist of 53 grids with duplicates removed.
 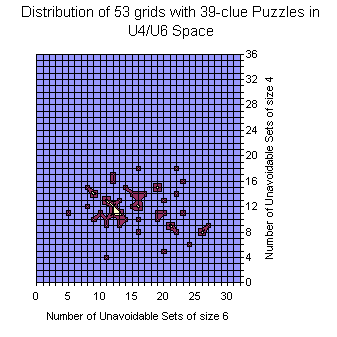
For 17-clues there are enough representatives and the picture is flat. The shape follows the general distribution. There are no grids with zero U6 but there are lots with zero U4.
There are islands too.
The most interesting is that the set is moved slightly to the lower U6 but significantly to the lower U4 coordinates. There are no grids with 20+ U4 sets.
The peak for the whole set is at (14,17), but for the 17-clues is at (14,7).
The average at U6 for all is 15.34 vs 14.76 for 17-clues.
The average at U4 is moved from 11.58 to 7.07.
The "Strangely Familiar" grid resides on coordinates (14,2) which is near to average by U6 but close to the zero at U4. Nevertheless in the same area for the 17-clues there are grids with less U4.
The 39-clues have 9 points with 2 grids, others are with single grid. Most grids reside (still) on islands.
Nevertheless, the averages are 15.66 at U6 and 11.64 at U4 which are close to the averages for the entire gridset.
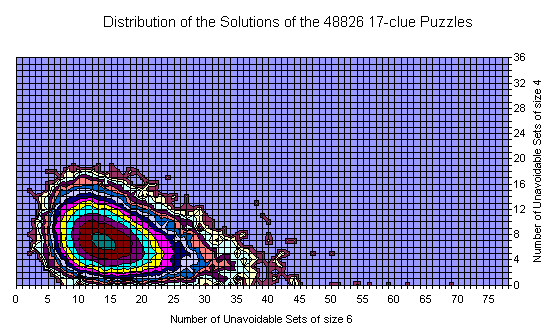
Back to U4 dimension
Here is the distribution of grids by U4 for the processed three gridsets.
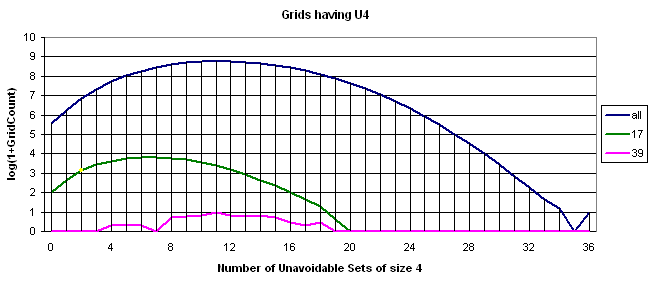
The smaller values for 17-clues are well visible. The yellow point represents the SF grid.
There is not much to say for 39-clues. It somehow follows the others.
The only differense between top curve here and the one published earlier is in the Y scale - no discontinuance at U4=35 here.
Data correctness
The count of U6 for all 53 39-clue grids have been independently calculated with Sudoku Checker tool. Three more grids have been observed during the development and debugging. Nevertheless bugs are possible and an independent confirmation of the result is always welcome.
MD |
|
| Back to top |
|
 |
| JPF
| | Joined: 05 Dec 2005 | | Posts: 29 | | : | | Location: Paris |
Items |
|
 Posted: Tue Mar 09, 2010 11:02 am Post subject: Posted: Tue Mar 09, 2010 11:02 am Post subject: |
 |
|
Impressive work !!
Congratulations.
| you wrote: | | Nevertheless bugs are possible and an independent confirmation of the result is always welcome |
If you tell me how (or where) you got the 5472730538 non equivalent grids, may be I could try to check independently your results.
JPF |
|
| Back to top |
|
 |
| dobrichev
| | Joined: 18 Dec 2009 | | Posts: 28 | | : | |
Items |
|
 Posted: Tue Mar 09, 2010 7:12 pm Post subject: Posted: Tue Mar 09, 2010 7:12 pm Post subject: |
 |
|
| JPF wrote: | Impressive work !!
Congratulations.
| you wrote: | | Nevertheless bugs are possible and an independent confirmation of the result is always welcome |
If you tell me how (or where) you got the 5472730538 non equivalent grids, may be I could try to check independently your results.
JPF |
Used Glenn Fowler's sudoku tool on Windows. The sudz compression somehow doesn't work for me. I downloaded some example (maybe from his site) and tried to decompress - no success, "invalid file content" or something similar. Then tried generating a compressed gridset. No success during the decompression, again with same error. Finally I generated uncompressed grids, and compressed them later to 10 bytes/grid using my own tool (see http://sites.google.com/site/dobrichev/sudokugrids/unav46count_winexe.zip).
| Code: | sudoku -gb1,3 > grids_001_014.txt
compress < grids_001_014.txt > grids_001_014.bin
del grids_001_014.txt
...
sudoku -gb173,416 > grids_173_416.txt
compress < grids_173_416.txt > grids_173_416.bin
del grids_173_416.txt
copy /b grids_001_014.bin+...+grids_173_416.bin grids.bin
unav46count < grids.bin > ua46_details.txt
|
Generating and compressing is single-thread so I ran 2 instances simulteneously to load my 2 processor cores. With some gaps it took 7 - 8 days to generate the set. A 54 GB file.
The counting pass (with built-in decompressing on the fly) tooks 6 hours. It automatically runs one thread per cpu core.
For the 17-clue set I did
| Code: | sudoku -f%C < puzzles_17.txt > 17_canon.txt
compress < 17_canon.txt > 17_canon.bin
unav46count < 17_canon.bin > 17unav_details.txt |
It will take 2 - 3 hours to cleanup a source code for the compressor/decompressor and unavoidable search procedures and publish it. I am postponing it until somebody shows interest.
I can share the 54GB file in e-mule p2p network. My uploading speed is about 200KB and the file could be downloaded within 4-5 days, about twice faster than the generating from scratch.
MD |
|
| Back to top |
|
 |
| dobrichev
| | Joined: 18 Dec 2009 | | Posts: 28 | | : | |
Items |
|
 Posted: Tue Mar 09, 2010 7:23 pm Post subject: Subject Change Posted: Tue Mar 09, 2010 7:23 pm Post subject: Subject Change |
 |
|
| Changed the topic's subject from "Unavoidable Sets of size 4" to "Solution Grids in U-Space (Unavoidable Sets)" |
|
| Back to top |
|
 |
| dobrichev
| | Joined: 18 Dec 2009 | | Posts: 28 | | : | |
Items |
|
 Posted: Sat Mar 13, 2010 6:29 am Post subject: More Grid Distribution Diagrams in U-space Posted: Sat Mar 13, 2010 6:29 am Post subject: More Grid Distribution Diagrams in U-space |
 |
|
Hello again,
The next pass trough all ED grids counted the grids with each possible combination of U-coordinates.
The result was a 5-dimentional array for U4, U6_1, U6_2, U6_3, and U6_4 coordinates. The range of the coordinates is respectively:
| Code: | Coordinate U4 U6_1 U6_2 U6_3 U6_4
Full Range 0..36 0..54 0..54 0..54 0..54
Gaps size 1 5 11 15 20
Compressed size 36 50 44 40 35 |
The data stored for each counter is a 31-bit unsigned integer, plus a 33-bit MinLex Index of the first (representative) grid.
The result is 36*50*44*40*35*8 = 887 040 000 bytes long file. The pass took 6h 45m.
Such pass was executed against the grids for the known 48826 17-clue puzzles, this time with duplicates removed.
The comparison in these planes was done:
- 3-digit / 2-digit unavoidables (U6_1 + U6_3, U6_2 + U6_4 + U4)
- 2-digit U6 / 2-digit U4 (U6_2 + U6_4, U4)
- U6_1 / U4
- U6_2 / U4
- U6_3 / U4
- U6_4 / U4
The source tabular values are in gridstat.txt and 17stat.txt.
On the pictures Z axis (colored) represents the count of the grids having exactly X and Y unavoidable sets. The Z scale is logarithmic, log10(1 + GridCount), the color scale is in 0.25 steps.
"Difference" is the count of the grids, scaled down by the factor "number of the grids having the same count of UA but also having at least one known 17-clue puzzle". In logarithmic scale this is a simple substraction.
Results and interpretation
All the distributions are relatively smooth.
The different types of U6 behave differently.
The disrtibution of 17-clue set has similar shape as for the whole set, but is scaled and moved closer to 0,0.
The most interesting result is that dividing the gridcount of the whole set to those for 17-clues subset (or substracting in the logarithmic scale) results in flattening of the intersection of the sets.
There are more detailed pictures for flattening in the U6_2/U4 plane. An attempt for interpretation is done at the end.
Grids Distribution in 3-digit / 2 digit plane
All Essentially Different Grids
Known Grids having 17-clue Puzzle
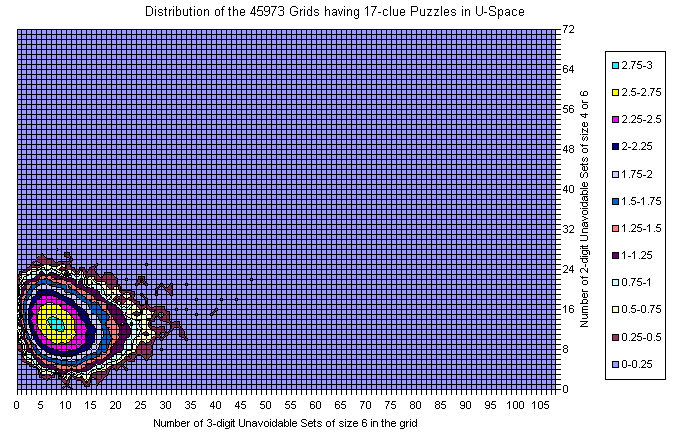
Difference
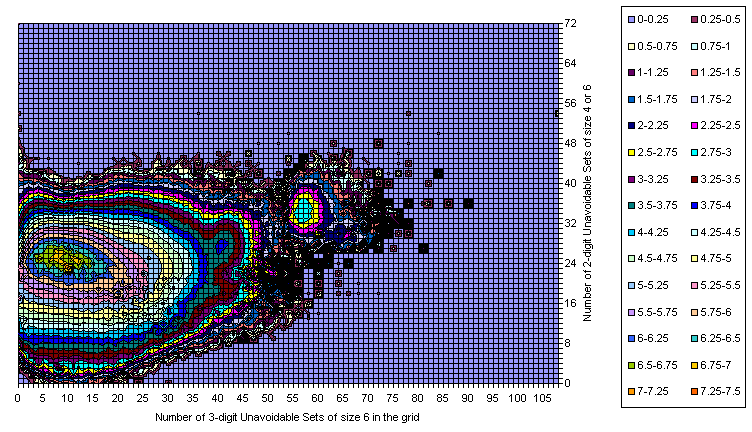
Grids Distribution in 2-digit U6 / 2 digit U4 plane
All Essentially Different Grids
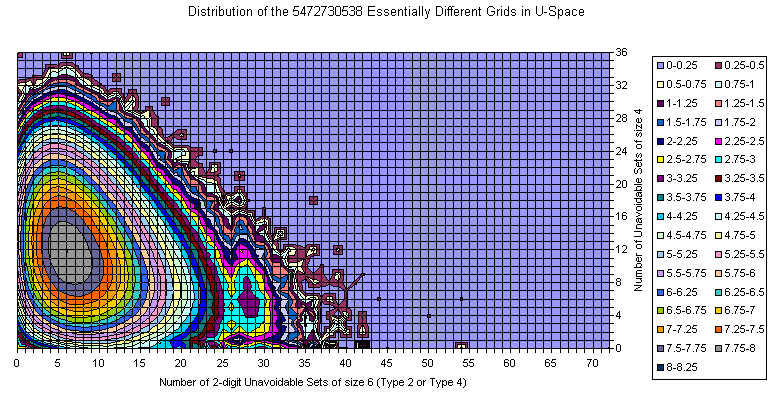
Known Grids having 17-clue Puzzle
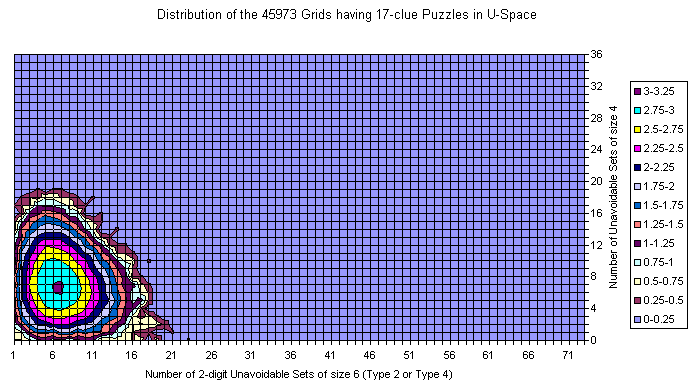
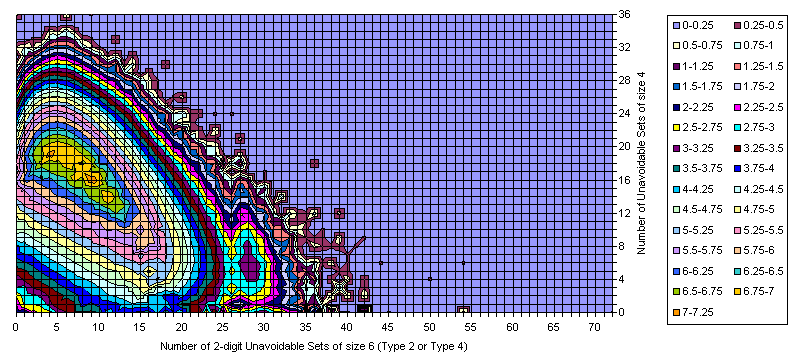
Difference
Grids Distribution in U6_1 / U4 plane
All Essentially Different Grids
Known Grids having 17-clue Puzzle
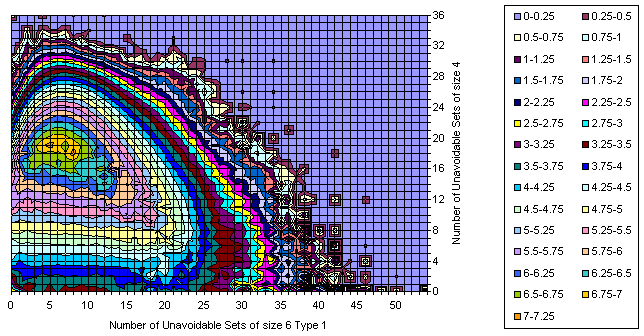
Difference
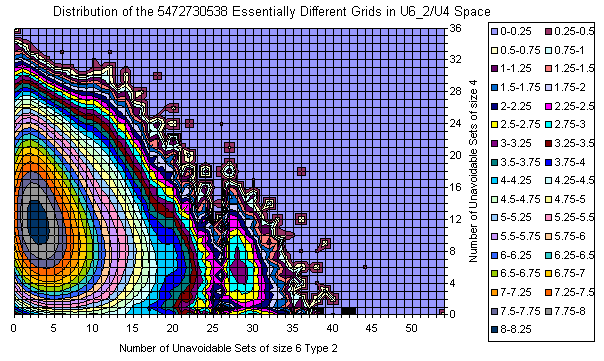
Grids Distribution in U6_2 / U4 plane
All Essentially Different Grids
Known Grids having 17-clue Puzzle
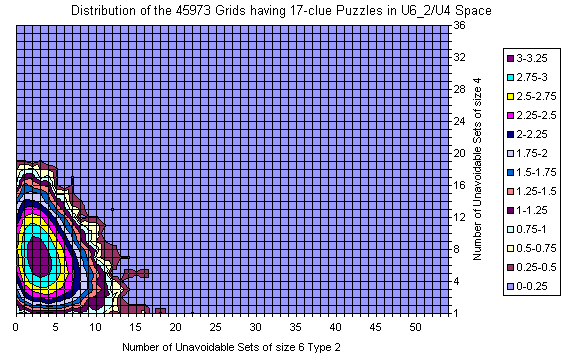
Difference
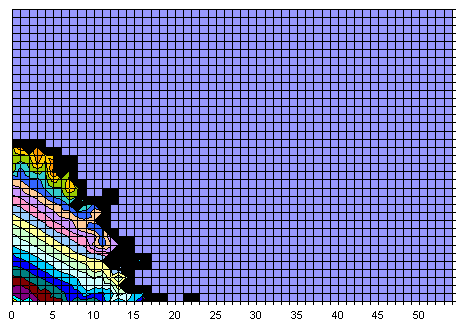
Here are 3D representations of the same graphics, plus the modified intersection between All and 17-clue grids.
The Z scale used in the intersection is If Z_all * Z_17 = 0 then 0 else log10(Z_all / Z_17), demonstrating there is no much noice coming from Z scale used in the other graphics.
All, Difference, and Intersection. View from bottom right in XY plane. It is easy to predict the location of several grids having still unknown 17-clue puzzles, isn't it?
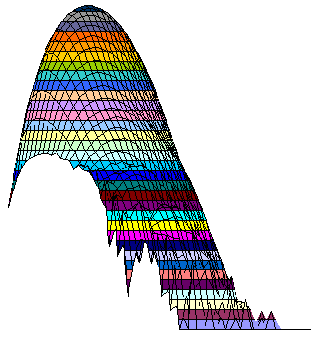  
Same rotation in XY plane but seen from 25 degrees up.
  
View from upper right in XY plane. The observer is nearly at the "flattened" plane.
Grids Distribution in U6_3 / U4 plane
All Essentially Different Grids
Known Grids having 17-clue Puzzle
Difference
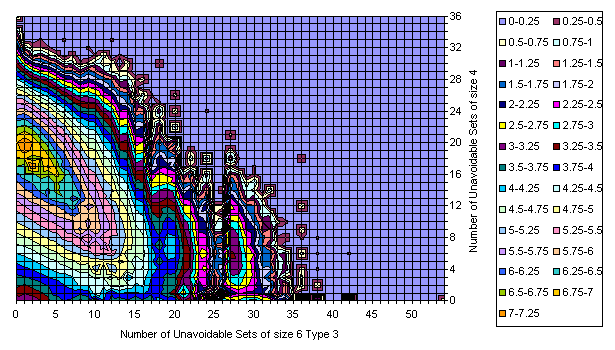
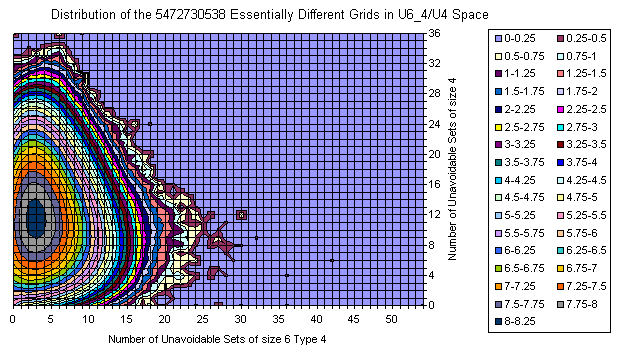
Grids Distribution in U6_4 / U4 plane
All Essentially Different Grids
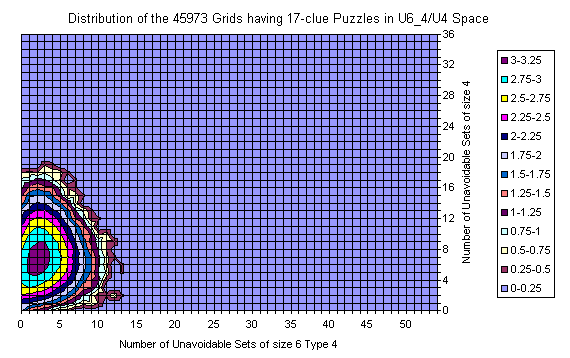
Known Grids having 17-clue Puzzle
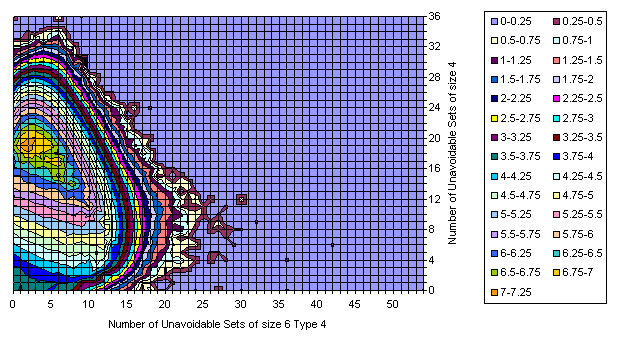
Difference
An attempt of flattening effect interpretation
Due to the nature of the sudoku grids (circular groups) the curvature of the manifold representing the grid count by various criteria should be a product of some factors, let say A, B, and C.
The subset of the grids having 17-clue puzzles should match some more restrictions (let say factor D).
Assume that D does not depend of A and B, but somehow contradicts most of the grids generated by C.
The resulting subset should modulated by the product of the A and B, and insignificantly by C.
Dividing the whole by a part representing some of the properties should nullify these properties. If our case the factor C will remain (at least parially), but the factors A and B will disappear, flattening the result.
Of course observable factors must affect the coordinates, in our case the number of unavoidable sets of size 4 and 6.
A closer look at the differences suggests that
- the cutting surface is flat, but is not exactly a plane.
- there are peaks in 17-clue subset which produce holes. See the resonance at (12,13) on U6_2 / U4 pictures.
- some of the peaks remaining after the substraction may be corrected by only one additional grid in 17-set, but others require 10-100.
- the vast majority of the grids is very close to the main peak. Deformation which the peripherial of the subset is causing to the peak of the whole set is much more significant than the middle of the flat surface produced by the peak of the subset.
- the flattened gridset has no physical meaning. It does not preserve the totals and its definition sounds too synthetic.
What if somebody considered to substract two subsets from the whole gridset?
Again, substracting in logarithmic scale is actually dividing, or scaling down.
Both the subsets must be independent. This means that
- they have to have no common coordinates at any point, or
- first s "substraction" of one of the subsets from the whole must be done, then the "difference" between both subsets must be substracted from the whole.
If there is data for a large enough 18-clue gridset available, it is a matter of hours such experiment to be done.
MD |
|
| Back to top |
|
 |
| dobrichev
| | Joined: 18 Dec 2009 | | Posts: 28 | | : | |
Items |
|
 Posted: Tue Mar 16, 2010 5:48 am Post subject: The Flattenning Source Posted: Tue Mar 16, 2010 5:48 am Post subject: The Flattenning Source |
 |
|
Hi,
The data files (see links above) are updated and several new values and tables are added.
Here is the property causing the flattening. It has been represented in 2 ways - once by assuming orthogonality between different types of unavoidables discussed, and second time assuming additivity.
In the following graphics the x axis represents the Radius of the cell in the 5-dimentional U-space, calculated as a square root of the sum of the squares of the coordinates.
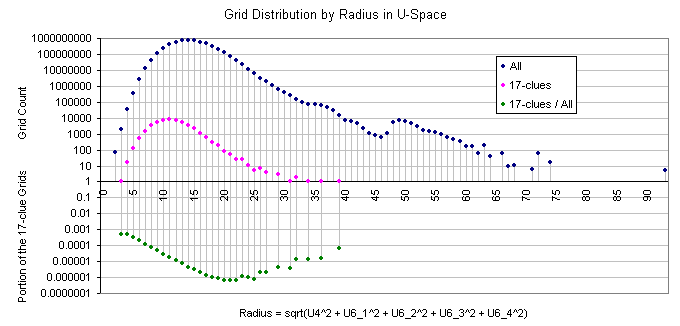
It is smoother than next graphics, which may be due to a) nature of the grids, or more likely b) the distance is not integer and the representation combines range of points into one value. The ratio is flat in the part where majority of the subset grids are located.
In the second graphics the additivity of the unavoidables of any kind is assumed and the x axis represents the sum of the unavoidables. The y axis is the same. The grid counts (not shown) have similar shape but are sharper near to the secondary maximums.
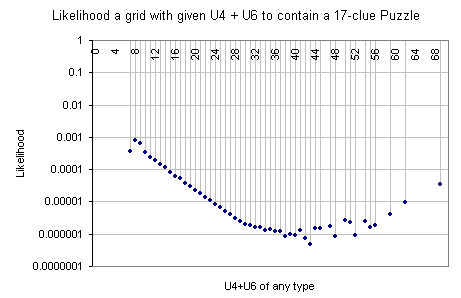
Both graphics are in logarithmic scale with uncertain points removed.
MD |
|
| Back to top |
|
 |
|
|
You cannot post new topics in this forum
You cannot reply to topics in this forum
You cannot edit your posts in this forum
You cannot delete your posts in this forum
You cannot vote in polls in this forum
|

Powered by phpBB © 2001, 2005 phpBB Group
Igloo Theme Version 1.0 :: Created By: Andrew Charron |









































