
|
| View previous topic :: View next topic |
| Author |
Message |
| Hakan
| | Joined: 09 Oct 2005 | | Posts: 10 | | : | |
Items |
|
 Posted: Sun Oct 09, 2005 9:50 pm Post subject: Posted: Sun Oct 09, 2005 9:50 pm Post subject: |
 |
|
| Lummox JR wrote: | | Now, in this situation you don't actually have a single conjugate set of colors. |
I think you have. Anyway, thanks for your explanation. Maybe I was not clear enough.
I think you explain multi-colors, and I understand how you can use multi-colors in this example. I also agree on your conclusion that you PLACE 7's in locations of the 'true' color 'B', (in stead of ELIMINATING the 'false' color 'b').
However, my first point is that I think you DON'T need multi-colors to solve this example. I think it is enough to use simple colors.
Using your notation, I can color cells without any A:s or a:s in the following way:
| Code: | ...|...|...
...|.*.|.*.
...|b*.|b..
-----------
..b|...|**.
...|B..|.b.
..B|.b.|...
-----------
...|...|...
...|...|...
...|...|... |
The 'b' in r5c8 should imply a 'b' in r3c7. Am I correct?
From this you can see (in row 3) that 'b' is the 'false' color, and 'B' must therefore be the 'true' color.
My second point is that it (sometimes, and at least in this example) could be dangerous to ELIMINATE the candidates of the 'false' color (as the Simple Sukoku program does). Instead, you should PLACE the candidates of the 'true' color. Am I correct?
/Hakan |
|
| Back to top |
|
 |
| Lummox JR
| | Joined: 07 Sep 2005 | | Posts: 202 | | : | |
Items |
|
 Posted: Mon Oct 10, 2005 6:04 am Post subject: Posted: Mon Oct 10, 2005 6:04 am Post subject: |
 |
|
| Quote: | | I think you explain multi-colors, and I understand how you can use multi-colors in this example. |
I think we're on different pages with the terminology, here. Simple coloring is merely coloring restricted to a single digit; multiple conjugate pairs are allowed. Multicoloring is actually a different technique which extends the concept across all digits at once.
| Quote: | | The 'b' in r5c8 should imply a 'b' in r3c7. Am I correct? |
No. There's nothing in (8,5) which would affect the value of (7,3) in any way. You can only color the conjugate of a colored cell, or else start up a new color pair. If (7,4) was a B, or (8,2) was a B, then you could color in (7,3) with b. However, there's no way to color in either of those cells with B because they don't have a conjugate b. They share a box or column or row with b, but merely sharing a house is not enough to spread colors.
This misplacement is the reason you're thinking it's dangerous to eliminate the false color. In truth it makes no difference whether you place true ones or eliminate false ones. Truth and falsehood are absolute in coloring. If one of the b cells is false, they're all false. I merely prefer to place the true ones because it saves time. |
|
| Back to top |
|
 |
| bart
| | Joined: 11 Aug 2005 | | Posts: 46 | | : | |
Items |
|
 Posted: Mon Oct 10, 2005 10:12 am Post subject: Posted: Mon Oct 10, 2005 10:12 am Post subject: |
 |
|
| Lummox JR wrote: | | Quote: | | I think you explain multi-colors, and I understand how you can use multi-colors in this example. |
I think we're on different pages with the terminology, here. Simple coloring is merely coloring restricted to a single digit; multiple conjugate pairs are allowed. Multicoloring is actually a different technique which extends the concept across all digits at once. |
and I quote agnus on this one:
Simple Colors
coloring one conjugate chain on a single candidate
Multi Colors
coloring more than one conjugate chain on a single candidate
Advanced Colors
coloring more than one conjugate chain on more than one candidate |
|
| Back to top |
|
 |
| Hakan
| | Joined: 09 Oct 2005 | | Posts: 10 | | : | |
Items |
|
 Posted: Mon Oct 10, 2005 6:02 pm Post subject: Posted: Mon Oct 10, 2005 6:02 pm Post subject: |
 |
|
| Lummox JR wrote: |
| Quote: | | The 'b' in r5c8 should imply a 'b' in r3c7. Am I correct? |
No.
...
You can only color the conjugate of a colored cell, or else start up a new color pair. |
OK. Thanks, I now see that I have extended the functionality of Simple Colors a bit too far. I forgot to stick to conjugate pairs all the way.
I just started with only one conjugate pair, and then tried to find out what happened if one of the candidates in that pair was true (for example 'B'). Then, I tried to find out what happened if the other candidate in that starting candidate pair was true (for example 'b'). If I then discovered a conflict in one of the colors, i.e. they shared the same group, this color was 'false'. This is why I thought a 'b' in r5c8 should imply a 'b' in r3c7. Actually it does, but now I understand that it is not called Simple Colors (and probably not anything with colors at all).
Is this perhaps another method? Please call it something else than trial and error. 
| Lummox JR wrote: |
This misplacement is the reason you're thinking it's dangerous to eliminate the false color. |
Yes, I guess your right.
/Hakan |
|
| Back to top |
|
 |
| Lummox JR
| | Joined: 07 Sep 2005 | | Posts: 202 | | : | |
Items |
|
 Posted: Mon Oct 10, 2005 6:57 pm Post subject: Posted: Mon Oct 10, 2005 6:57 pm Post subject: |
 |
|
Over at the SadMan page, simple coloring is defined as coloring with a single digit, and specifically includes cases of multiple conjugate pairs. The terms multicoloring and supercoloring are used interchangeably, which agrees more with common usage in other threads both here and on the players forum (where ultracoloring is another name for those two methods). This is from the end of the page, where single-conjugate and multiple-conjugate forms have already both been discussed:
| Quote: | | This technique is known as "simple colouring." There is also "multicolouring" or "supercolouring", a technique that makes deductions by combining the implications from conjugates of all candidates for all cells, although this technique is beyond the ability of most, if not all, human solvers. |
Now granted, I don't agree with all the definitions on that page and it doesn't show how to link exclusions to their full potential, but overall I think it has the right idea. Coloring with one conjugate is only barely easier than using more than one, because of the low number of colors usually involved.
And coloring even as described algorithmically on this forum goes right to the multiple-conjugate approach. Nick70 uses the term "simple coloring" in this post to refer to multi-conjugate forms, and advanced coloring to mean the same as supercoloring. (Of course in that same post he says swordfish is just a special case of coloring, which it isn't. Swordfish is a subset test, and not all forms of it can be handled with coloring. But then, that seemed to be a common misconception a few months ago.) AMcK has also used the term "simple coloring" to refer to multi-conjugate sets. That same thread in fact only delineates between simple and advanced coloring, the latter being the technique that is often better known as supercoloring or ultracoloring. Last but not least, this supremely helpful post from Doug Bowman also refers to the multiple-conjugate method as just "coloring".
So with respect, I disagree with angus's distinction here and would instead consider the single-conjugate case to be dirt-simple coloring. Clearly labeling simple coloring as only using one color pair is not in keeping with common parlance. The term "simple" came along apparently just to separate single-digit coloring from the full advanced form which is supercoloring. |
|
| Back to top |
|
 |
| rkral
| | Joined: 21 Oct 2005 | | Posts: 233 | | : | |
Items |
|
 Posted: Fri Oct 28, 2005 12:15 pm Post subject: Re: Coloring Posted: Fri Oct 28, 2005 12:15 pm Post subject: Re: Coloring |
 |
|
From back on Aug 29 ...
| angusj wrote: | | lennyh wrote: | | Would you suggest that your helpful explanation in todays posting regarding multicolors001.ss is an example or particular case of either rule 1 or rule 2, or would you rather suggest that it is a separate rule -- perhaps specific to the multi-color consideration? |
Yes, it's a separate multi-color rule, not covered by simple colors. |
Do you have a few links to explanations of other rules?
Of current interest is your undefined150.ss, which at state ... | Code: |
*-----------*
|.37|2.8|1.5|
|2.1|5..|8.3|
|.5.|.31|72.|
|---+---+---|
|.2.|345|...|
|193|726|584|
|..5|189|.3.|
|---+---+---|
|.14|9..|.58|
|582|.1.|...|
|3.9|85.|4..|
*-----------* |
... eventually produces coloring hint ... | Code: |
. . . | . . . | . . .
. . . | . . . | . . .
. . B | a . . | . . .
- - - + - - - + - - -
6 . b | . . . | . . .
. . . | . . . | . . .
. . . | . . . | . . .
- - - + - - - + - - -
A . . | . a . | . . .
. . . | A . . | . . .
. a . | . . . | . . .
|
'A' is amber, 'a' is pink, 'B' is blue, and 'b' is green in SS coloring.
There are many other candidates of digit 6, but only the hinted exclusion at r4c1 is shown above.
If we represent the uncolored r4c1 by color x, we have (true) A excluding (true) x, and (true) b excluding (true) x. Using notation I've seen elsewhere: A!x and b!x. By inspection of the color grid, we have a!B in row 3. And by definition, B!b, b!B, A!a, and a!A.
"Chaining" the above: a!B, B!b, and b!x.
On the one hand A!x. On the other hand, per the above, a!x. Therefore, x = 6 cannot be true.
Expressed in words, it seems as if a candidate at the intersection of a non-conjugate pair Ab (colored your amber/green) can be eliminated if non-conjugate pair aB (colored your pink/blue) exists anywhere else on the color grid.
TIA for any link(s) you are inclined to provide, Ron |
|
| Back to top |
|
 |
| angusj
Site Admin
 | | Joined: 18 Jun 2005 | | Posts: 406 | | : | |
Items |
|
 Posted: Fri Oct 28, 2005 12:44 pm Post subject: Re: Coloring Posted: Fri Oct 28, 2005 12:44 pm Post subject: Re: Coloring |
 |
|
| rkral wrote: | Do you have a few links to explanations of other rules?
Of current interest is your undefined150.ss |
Hi Ron.
There are 2 types of what I call multi-colors. When filtering on a specific candidate and finding to 2 seperate conjugate chains (labelled A+,A- & B+,B-) ...
Type 1: If A+ shares a group with B+ and B- then A+ must be the false candidate since either B+ or B- must be true.
Example of Type 1:
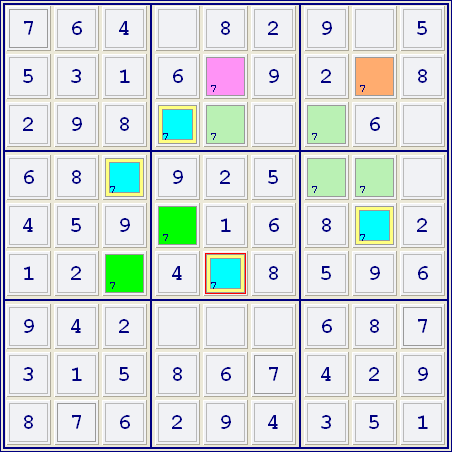
Filtering on 7s and given that Blue & Bright Green are conjugate cells as are the Pink and Orange cells - then since either Pink or Orange must be 'true', then the Blue cells must be the 'false' cells since they share a group with both Pink and Orange. Candidate 7 can be excluded from all Blue cells.
Type 2: If A+ shares a group with B+ then any cell with the given candidate and sharing a group with both A- and B- can have that candidate excluded. Reason: Since A+ and B+ can't both be true, then either one or both of A- and B- must be true. Therefore any cell sharing a group with both A- and B- can safely have that candidate excluded.
Example of Type 2:
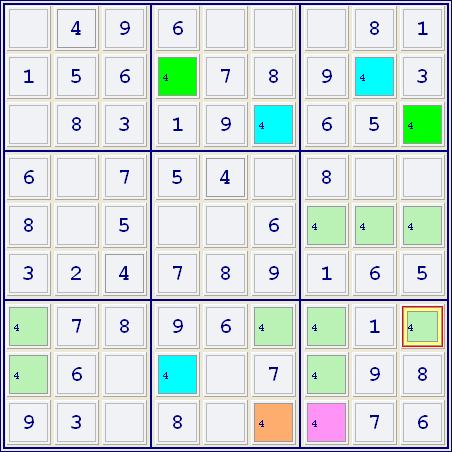
Filtering on 4s and given that Blue & Bright Green are conjugate cells as are the Pink and Orange cells - then the Orange and Blue cells can't both be 'true' cells as they share a group. Therefore one or both of the Pink and Bright Green cells must be 'true' and, consequently, any cells which share a group with both Pink and Bright Green cells (ie r7c9) can have candidate 4 removed from that cell.
(Undefined150.ss puzzle is also an example of Multicolors Type 2 .) |
|
| Back to top |
|
 |
| rkral
| | Joined: 21 Oct 2005 | | Posts: 233 | | : | |
Items |
|
 Posted: Fri Oct 28, 2005 3:43 pm Post subject: Re: Coloring Posted: Fri Oct 28, 2005 3:43 pm Post subject: Re: Coloring |
 |
|
Angus, thanks for your reply.
| angusj wrote: | If A+ shares a group with B+ and B- then A+ must be the false candidate since either B+ or B- must be true.
[snip] and
... since either Pink or Orange must be 'true', then the Blue cells must be the 'false' cells since they share a group with both Pink and Orange |
So for your example of 'Type 1', Blue is A+, Green is A- by elimination, and B+ and B- are arbitrarily Pink and Orange?
| angus wrote: | Since A+ and B+ can't both be true, then either one or both of A- and B- must be true.
[snip] and
... the Orange and Blue cells can't both be 'true' cells as they share a group. |
So for your example of Type 2', Orange and Blue are arbitrarily A+ and B+, and A- and B- follow depending on the conjugate color pairing?
It looks like your A+, A-, B+, and B- symbols correspond respectively to the A, a, B, and b symbols I used. Why would anyone wish to use two character symbols when one character indicates the same thing? |
|
| Back to top |
|
 |
| Kombat
| | Joined: 23 Jan 2006 | | Posts: 1 | | : | |
Items |
|
 Posted: Mon Jan 23, 2006 9:56 pm Post subject: Posted: Mon Jan 23, 2006 9:56 pm Post subject: |
 |
|
| Code: | *-----------*
|.54|...|8..|
|.6.|...|.1.|
|..8|.65|4.3|
|---+---+---|
|...|1.4|.8.|
|...|.9.|...|
|.1.|6.3|...|
|---+---+---|
|7.2|51.|6..|
|.4.|...|.9.|
|..9|...|23.|
*-----------*
*-----------*
|.54|..1|86.|
|.67|...|.1.|
|1.8|.65|4.3|
|---+---+---|
|..6|154|38.|
|..3|.9.|156|
|.15|6.3|...|
|---+---+---|
|732|519|648|
|641|...|.9.|
|589|..6|231|
*-----------*
*--------------------------------------------------------------------*
| 239 5 4 | 2379 237 1 | 8 6 279 |
| 239 6 7 | 23489 248 28 | 59 1 259 |
| 1 29 8 | 279 6 5 | 4 27 3 |
|----------------------+----------------------+----------------------|
| 29 279 6 | 1 5 4 | 3 8 27 |
| 48 27 3 | 278 9 278 | 1 5 6 |
| 48 1 5 | 6 278 3 | 79 27 2479 |
|----------------------+----------------------+----------------------|
| 7 3 2 | 5 1 9 | 6 4 8 |
| 6 4 1 | 238 238 28 | 57 9 57 |
| 5 8 9 | 47 47 6 | 2 3 1 |
*--------------------------------------------------------------------*
|
Why is this not a multi-colors scenario? I'm looking at 3's and R1C1 and R2C1 are conjugates, and R8C4 and R8C5 are conjugates. I tried to remove the 3 from R1C5 but got an invalid move error. These are two separate chains and R1C5 share a group with each chain.
Thanks,
Karl |
|
| Back to top |
|
 |
| Ruud
Site Admin
 | | Joined: 17 Sep 2005 | | Posts: 708 | | : | | Location: Netherlands |
Items |
|
 Posted: Mon Jan 23, 2006 11:06 pm Post subject: Posted: Mon Jan 23, 2006 11:06 pm Post subject: |
 |
|
Hi Karl,
in multi-coloring, there is no rule that excludes candidates based on the fact that they share a group with 2 separate coloring chains.
- A candidate that shares a group with 2 colors of a single chain can be removed.
- A candidate that shares a group with 2 separate chains, of which the complement colors also share a group, can be removed.
- The candidates in a chain for which the color appears twice in a group can also be removed.
- Then there is the option to link more than 2 chains, but that is certainly not the case here.
Your conclusion is wrong. You should not remove this candidate.
Ruud.
_________________
Meet me at sudocue.net |
|
| Back to top |
|
 |
| orlp
| | Joined: 25 Feb 2006 | | Posts: 4 | | : | |
Items |
|
 Posted: Sat Feb 25, 2006 11:20 am Post subject: Re: Coloring Posted: Sat Feb 25, 2006 11:20 am Post subject: Re: Coloring |
 |
|
| angusj wrote: | | rkral wrote: | Do you have a few links to explanations of other rules?
Of current interest is your undefined150.ss |
Hi Ron.
There are 2 types of what I call multi-colors. When filtering on a specific candidate and finding to 2 seperate conjugate chains (labelled A+,A- & B+,B-) ...
Type 1: If A+ shares a group with B+ and B- then A+ must be the false candidate since either B+ or B- must be true.
Example of Type 1:

Filtering on 7s and given that Blue & Bright Green are conjugate cells as are the Pink and Orange cells - then since either Pink or Orange must be 'true', then the Blue cells must be the 'false' cells since they share a group with both Pink and Orange. Candidate 7 can be excluded from all Blue cells.
Type 2: If A+ shares a group with B+ then any cell with the given candidate and sharing a group with both A- and B- can have that candidate excluded. Reason: Since A+ and B+ can't both be true, then either one or both of A- and B- must be true. Therefore any cell sharing a group with both A- and B- can safely have that candidate excluded.
Example of Type 2:

Filtering on 4s and given that Blue & Bright Green are conjugate cells as are the Pink and Orange cells - then the Orange and Blue cells can't both be 'true' cells as they share a group. Therefore one or both of the Pink and Bright Green cells must be 'true' and, consequently, any cells which share a group with both Pink and Bright Green cells (ie r7c9) can have candidate 4 removed from that cell.
(Undefined150.ss puzzle is also an example of Multicolors Type 2 .) |
I think one may be able to deal with Type 2 multicolor solutions more easily using an asymmetric version of single coloring.
In the diagram below I hav marked only the '4' candidates of angus' example:
+ + + |+ + + |+ + +
+ + + |4 + + |+ 4 +
+ + + |+ + 4g|+ + 4b
--------------------------
+ + + |+ + + |+ + +
+ + + |+ + + |4 4 4
+ + + |+ + + |+ + +
-------------------------
4 + + |+ + 4b!4 + 4*
4 + + |4 + + |4 + +
+ + + |+ + 4b|4g+ +
Definitions:
A '(strong) conjugate' of a cell shares a row, column or block with the cell in such a way that the two cells are the only ones containing a the given candidate (4)
A 'weak conjugate' of a candidate cell shares a row, column or block with the cell, and both have the candidate (4). There need not be only two in the relevant row column or block.
Rule:
Choose a cell and mark it blue (b) I chose r3c9
Iterate the following to steps:
Mark strong conjugates of blue cells green (g).
Mark weak conjugates of green cells blue (b).
If a cell is weakly conjugate to the initial cell and a green cell (*) then the candidate can be eliminated.
In the example the sequence is
r3c9 b
r3c6 g
r7c6 and r9c6 b
r9c7 g
Now r7c9 is weakly conjugate to r3c9 and r9c7 and so can be eliminated.
Justification:
Let blue coloring correspond to the assumption "the candidate is not in this cell" and green coloring correspond to the assumption "the candidate is in this cell". Then the rules follow the logical consequences of assuming the candidate is not in the first cell colored blue. The pattern corresponds to the statement (in the example) "If 4 is not in r3c9 it must be in r9c7. Therefore it cannot be in r7c9"
The chain of conditions can be started at any blue cell that is a strong conjugate of its preceding green cell.
I suspect but have not proved that all type 2 multicolor problems yield to this attack.
Oliver Pretzel |
|
| Back to top |
|
 |
| rkral
| | Joined: 21 Oct 2005 | | Posts: 233 | | : | |
Items |
|
 Posted: Sat Feb 25, 2006 7:30 pm Post subject: Re: Coloring Posted: Sat Feb 25, 2006 7:30 pm Post subject: Re: Coloring |
 |
|
| orlp wrote: | In the example the sequence is
r3c9 b
r3c6 g
r7c6 and r9c6 b
r9c7 g
Now r7c9 is weakly conjugate to r3c9 and r9c7 and so can be eliminated.
|
While the elimination is valid, the technique is not. It's a "lucky accident.
The coloring above is valid until "r9c7 g". That step is NOT valid because r9c7 cannot see BOTH blue cells r7c6 AND r9c6. However, you could validly color r8c4 green and continue to r8c1 and r7c1 ... but it then ends there.
It appears you are attempting to use a "grouped candidates" technique, a technique that is fraught with hazards. It should not be attempted by a sudoku novice IMO.
Ron
P.S. By definition, conjugates are strongly linked. Therefore "weak conjugate" is contradictory and "strong conjugate" is redundant. |
|
| Back to top |
|
 |
| orlp
| | Joined: 25 Feb 2006 | | Posts: 4 | | : | |
Items |
|
 Posted: Sun Feb 26, 2006 1:15 pm Post subject: Re: Coloring Posted: Sun Feb 26, 2006 1:15 pm Post subject: Re: Coloring |
 |
|
| rkral wrote: | | orlp wrote: | In the example the sequence is
r3c9 b
r3c6 g
r7c6 and r9c6 b
r9c7 g
Now r7c9 is weakly conjugate to r3c9 and r9c7 and so can be eliminated.
|
While the elimination is valid, the technique is not. It's a "lucky accident.
The coloring above is valid until "r9c7 g". That step is NOT valid because r9c7 cannot see BOTH blue cells r7c6 AND r9c6. However, you could validly color r8c4 green and continue to r8c1 and r7c1 ... but it then ends there.
It appears you are attempting to use a "grouped candidates" technique, a technique that is fraught with hazards. It should not be attempted by a sudoku novice IMO.
Ron
P.S. By definition, conjugates are strongly linked. Therefore "weak conjugate" is contradictory and "strong conjugate" is redundant. |
The technique *is* valid and the result is *not* an accident, but maybe I have explained it badly. I am advocating an extension of the standard colouring technique, which I call 'asymmetric'. For this extension it is important to understand the difference between weakly conjugate and strongly conjugate.
Weakly conjugate squares share a row, column or block
Strongly conjugate squares share a row column or block and are the only two squares in that row, column or block containing the relevat candidate.
Observe that if the candidate is not the value of a square X, we can concludee that it must be the value of any strongly conjugate square (but we cannot conclude anything about weakly conjugate squares).
On the other hand if the candidate is the value of a square X, then it is not the value of any weakly conjugate square.
My asymmetric colouring argument is based on the observation that a candidate can be eliminated from square A if it is weakly conjugate to two squares B and C, such that the candidate must be the value of one of B and C.
So we are searching for squares B and C that satisfy "if candidate n is not the value of B then it must be the value of C".
We start with an arbitrary square B and apply the hypothesis "the candidate is not the value of this square" (which may be true or false) colouring the square blue to mark this.
We can now deduce that under the hypothesis the candidate must be the value of all strongly conjugate squares of B and we colour them green to denote this.
Now the candidate cannot be the value in any square weakly conjugate to a green square. So we colour all these squares blue.
We continue in this fashion alternately colouring squers green and blue using strong conjugacy when we colour squares green and weak conjugacy when we colour squares blue.
If we find a square D weakly conjugate to a green square C and also to our starting square B., then we can elimiante the candidate from D,
because if the hypothesis that the value of B is not the candidate holds,
then the value of C must be the candidate, and if the hypothesis does not hold then the value of B is the candidate. In either case the value of D is not the candidate.
To go back to the example
Hypothesis r3c9 is not 4 (which may be true or false)
Colour r3c9 blue
Under the hypothesis r3c6 is 4. Colour it green.
Under the hypothesis neither r7c6 not r9c6 is 4. Colour them blue.
Under the assumption r9c7 must be 4. Colour it green.
Hence one of r3c9 and r9c7 must be 4, and so r7c9 can be elimated,
I hope this clarifies the argument, and makes it clear that it is always valid.
Of course one may feel that this technique verges on a forcing chains type argument. But there is a difference. In forcing chains we have to build two or more distinct logical chains, one for each candidate in the initial square. Asymmetric colouring requires only one chain and only two colours.
Oliver |
|
| Back to top |
|
 |
| rkral
| | Joined: 21 Oct 2005 | | Posts: 233 | | : | |
Items |
|
 Posted: Sun Feb 26, 2006 2:06 pm Post subject: Re: Coloring Posted: Sun Feb 26, 2006 2:06 pm Post subject: Re: Coloring |
 |
|
| orlp wrote: | To go back to the example
Hypothesis r3c9 is not 4 (which may be true or false)
Colour r3c9 blue
Under the hypothesis r3c6 is 4. Colour it green.
Under the hypothesis neither r7c6 not r9c6 is 4. Colour them blue.
Under the assumption r9c7 must be 4. Colour it green.
Hence one of r3c9 and r9c7 must be 4, and so r7c9 can be elimated,
I hope this clarifies the argument, and makes it clear that it is always valid. |
You should be able to follow the links in both the clockwise (CW) and counter-clockwise (CCW) directions to prove the elimination. Starting at r3c9 and going CCW, it's fine. Using "->" for the word "implies":
r3c9<>4 -> r3c6=4 -> r9c6<>4 -> r9c7=4
In the CW direction, you need ...
r9c7<>4 -> r9c6=4 -> r3c6<>4 -> r3c9=4
... which is only possible if the highlighted link is a strong link, i.e., due to a conjugate pair. In the manner you have colored your example, that strong link does not exist, because BOTH blue candidates in box 8 don't see the false candidate in r9c7. You are unwittingly using multicoloring without showing the technique as multicoloring.
Keep using your technique as you've described, and guaranteed, you will eventually run into an instance where it doesn't work.
Ron |
|
| Back to top |
|
 |
| orlp
| | Joined: 25 Feb 2006 | | Posts: 4 | | : | |
Items |
|
 Posted: Tue Feb 28, 2006 10:55 am Post subject: Re: Coloring Posted: Tue Feb 28, 2006 10:55 am Post subject: Re: Coloring |
 |
|
| rkral wrote: | | orlp wrote: | To go back to the example
Hypothesis r3c9 is not 4 (which may be true or false)
Colour r3c9 blue
Under the hypothesis r3c6 is 4. Colour it green.
Under the hypothesis neither r7c6 not r9c6 is 4. Colour them blue.
Under the assumption r9c7 must be 4. Colour it green.
Hence one of r3c9 and r9c7 must be 4, and so r7c9 can be elimated,
I hope this clarifies the argument, and makes it clear that it is always valid. |
You should be able to follow the links in both the clockwise (CW) and counter-clockwise (CCW) directions to prove the elimination. Starting at r3c9 and going CCW, it's fine. Using "->" for the word "implies":
r3c9<>4 -> r3c6=4 -> r9c6<>4 -> r9c7=4
In the CW direction, you need ...
r9c7<>4 -> r9c6=4 -> r3c6<>4 -> r3c9=4
... which is only possible if the highlighted link is a strong link, i.e., due to a conjugate pair. In the manner you have colored your example, that strong link does not exist, because BOTH blue candidates in box 8 don't see the false candidate in r9c7. You are unwittingly using multicoloring without showing the technique as multicoloring.
Keep using your technique as you've described, and guaranteed, you will eventually run into an instance where it doesn't work.
Ron |
On the contrary - I have *proved* that it always works.
There is absolutely no need for symmetry in the chain. The logical implication
If (not B) then C
is, on its own, sufficient to prove that one of B and C must be true.
My asymmetric chain *proves* that if r3c9 is not 4 then r9c7 must be 4.
That is all that is required to eliminate r7c9 which is conjugate to both r3c9 and and r9c7.
It is entirely unnecessary to prove also that if r9c7 is not 4 then r3c9 is 4 since that follows by logical equivalence (though not, as you rightly say. directly from the colouring)
Oliver |
|
| Back to top |
|
 |
|
|
You cannot post new topics in this forum
You cannot reply to topics in this forum
You cannot edit your posts in this forum
You cannot delete your posts in this forum
You cannot vote in polls in this forum
|

Powered by phpBB © 2001, 2005 phpBB Group
Igloo Theme Version 1.0 :: Created By: Andrew Charron |





