| View previous topic :: View next topic |
| Author |
Message |
| angusj
Site Admin
 | | Joined: 18 Jun 2005 | | Posts: 406 | | : | |
Items |
|
 Posted: Thu Sep 08, 2005 10:36 am Post subject: Posted: Thu Sep 08, 2005 10:36 am Post subject: |
 |
|
| AMcK wrote: | Immediate contradiction in r4c3 B=False, A=True
|
OK, I don't understand what you mean by the above. However, this is what I come up with based on your clue re cell r4c3:
Filtering on 1's
| Code: | *-----------*
|...|...|...|
|...|...|...|
|...|...|...|
|---+---+---|
|..G|...|...|
|..B|...|..G|
|...|...|.B.|
|---+---+---|
|...|...|...|
|...|...|...|
|...|...|...|
*-----------* |
Filtering on 9's
| Code: | *-----------*
|...|...|...|
|..G|..B|...|
|...|..G|B..|
|---+---+---|
|..B|...|...|
|...|...|...|
|...|...|GB.|
|---+---+---|
|...|...|...|
|...|...|...|
|...|...|...|
*-----------* |
Observing cells r4c3 and r6c8, the in 1's these cells are conjugates but the 9s must be the same which is a contradiction if these two cells contain only 1s & 9s. Therefore at least one of these cell must be neither which leaves r4c3 = 4 as the only alternative. (Simple solving beyond that.)
Edit: OK, I think I understand your somewhat cryptic summary now:
1A & 1B are conjugates (implicitly) and 1A & 9B are conjugates (r6c8).
Therefore, both 9B and 1B are either both true or both false.
Hence, given 1B excludes 9B (r4c3), they both must be false. |
|
| Back to top |
|
 |
| Nick70
| | Joined: 08 Jun 2005 | | Posts: 160 | | : | |
Items |
|
 Posted: Thu Sep 08, 2005 2:01 pm Post subject: Posted: Thu Sep 08, 2005 2:01 pm Post subject: |
 |
|
| angusj wrote: | | Both puzzles 4 & 6 required only one use of simple colors as illustrated above |
Both Turbots btw  |
|
| Back to top |
|
 |
| Nick70
| | Joined: 08 Jun 2005 | | Posts: 160 | | : | |
Items |
|
 Posted: Thu Sep 08, 2005 2:05 pm Post subject: Posted: Thu Sep 08, 2005 2:05 pm Post subject: |
 |
|
| AMcK wrote: | | That's a neat use of simple colouring that I haven't used before. |
Come on, how can you say that? We have been using it since day 1. |
|
| Back to top |
|
 |
| AMcK
| | Joined: 07 Apr 2005 | | Posts: 89 | | : | | Location: Cambridge |
Items |
|
 Posted: Thu Sep 08, 2005 2:55 pm Post subject: Posted: Thu Sep 08, 2005 2:55 pm Post subject: |
 |
|
| angusj wrote: | | AMcK wrote: | Immediate contradiction in r4c3 Y=False, X=True
|
OK, I don't understand what you mean by the above. |
Hi Angus
I'm very impressed by how much you're managing to get out of simple colouring and will revisit that to see how much can be gained in "human friendly" solving methods.
If you take "Ultra 2"
| Code: | 7..¦ .6.¦ 3.8
18.¦ 32.¦ ..6
65.¦ 8..¦ .4.
---+----+----
...¦ .3.¦ .5.
...¦ 9.7¦ ...
.6.¦ .5.¦ ...
---+----+----
.2.¦ ..3¦ .85
3..¦ .96¦ .24
4.5¦ .1.¦ ..9 |
and do the standard reductions to | Code: | 7 49 2 ¦ 14 6 5 ¦ 3 19 8
1 8 49 ¦ 3 2 49 ¦ 5 7 6
6 5 3 ¦ 8 7 19 ¦ 29 4 12
------------+-------------+-------------
28 49 149 ¦ 6 3 124 ¦ 48 5 7
5 3 14 ¦ 9 8 7 ¦ 24 6 12
28 6 7 ¦ 14 5 124 ¦ 489 19 3
------------+-------------+-------------
9 2 6 ¦ 7 4 3 ¦ 1 8 5
3 1 8 ¦ 5 9 6 ¦ 7 2 4
4 7 5 ¦ 2 1 8 ¦ 6 3 9 |
For convenience, I label each possible on the grid using a lower case letter specific to each possible i.e. in r1c1 the "a" in 4a isn't a colour and is initially unrelated to the "a" in 9a. | Code: | 7 4a9a 2 ¦ 1a4b 6 5 ¦ 3 1b9b 8
1 8 4c9c ¦ 3 2 4d9d ¦ 5 7 6
6 5 3 ¦ 8 7 1c9e ¦ 2a9f 4 1d2b
-----------------+---------------+------------------
2c8a 4e9g 1e4f9h ¦ 6 3 1f2d4g ¦ 4h8b 5 7
5 3 1g4i ¦ 9 8 7 ¦ 2e4j 6 1h2f
2g8c 6 7 ¦ 1i4k 5 1j2h4l ¦ 4m8d9i 1k9j 3
-----------------+---------------+------------------
9 2 6 ¦ 7 4 3 ¦ 1 8 5
3 1 8 ¦ 5 9 6 ¦ 7 2 4
4 7 5 ¦ 2 1 8 ¦ 6 3 9 |
Let's start colouring the possibles using the conjugate relationships in the grid, this time using capital letters which really do have significance for all possibles. Start with r1c2 and colour 4a as 4X and 9a as 9Y, noting that X and Y are now conjugate colours i.e. one of them must be true and the other must be false - we just don't yet know which.
We then propagate the colours X and Y across the grid e.g. 4b in r1c4 is conjugate to 4X in r1c2 and can be coloured 4Y, 1a in r1c4 is conjugate to 4Y in r1c2 and can be coloured 1X.
Here's the initial set of conjugates, all of which are obvious, to guide the colouring of the grid using X and Y | Code: | r1: 1a conjugates 1b
r1: 4a conjugates 4b
r1: 9a conjugates 9b
r2: 4c conjugates 4d
r2: 9c conjugates 9d
r3: 1c conjugates 1d
r3: 2a conjugates 2b
r3: 9e conjugates 9f
r4: 9g conjugates 9h
r5: 1g conjugates 1h
r5: 2e conjugates 2f
r5: 4i conjugates 4j
r6: 9i conjugates 9j
c2: 4a conjugates 4e
c3: 9c conjugates 9h
c4: 1a conjugates 1i
c4: 4b conjugates 4k
c7: 9f conjugates 9i
c8: 1b conjugates 1k
c8: 9b conjugates 9j
c9: 1d conjugates 1h
c9: 2b conjugates 2f
b1: 4a conjugates 4c
b1: 9a conjugates 9c
b2: 1a conjugates 1c
b2: 4b conjugates 4d
b2: 9d conjugates 9e
b3: 1b conjugates 1d
b3: 2a conjugates 2b
b6: 1h conjugates 1k
r1c2: 4a conjugates 9a
r1c4: 1a conjugates 4b
r1c8: 1b conjugates 9b
r2c3: 4c conjugates 9c
r2c6: 4d conjugates 9d
r3c6: 1c conjugates 9e
r3c7: 2a conjugates 9f
r3c9: 1d conjugates 2b
r4c2: 4e conjugates 9g
r5c3: 1g conjugates 4i
r5c7: 2e conjugates 4j
r5c9: 1h conjugates 2f
r6c8: 1k conjugates 9j |
This takes us to the intermediate state
| Code: |
7 4X9Y 2 ¦ 1X4Y 6 5 ¦ 3 1Y9X 8
1 8 4Y9X ¦ 3 2 4X9Y ¦ 5 7 6
6 5 3 ¦ 8 7 1Y9X ¦ 2X9Y 4 1X2Y
-----------------+---------------+-----------------
2c8a 4Y9X 1e4f9Y ¦ 6 3 1f2d4g ¦ 4h8b 5 7
5 3 1X4Y ¦ 9 8 7 ¦ 2Y4X 6 1Y2X
2g8c 6 7 ¦ 1Y4X 5 1j2h4 ¦ 4m8d9X 1X9Y 3
-----------------+---------------+-----------------
9 2 6 ¦ 7 4 3 ¦ 1 8 5
3 1 8 ¦ 5 9 6 ¦ 7 2 4
4 7 5 ¦ 2 1 8 ¦ 6 3 9 |
where the capital letters X, Y denote coloured possibles and the small letters denote possibles not yet coloured. If we can prove that X is true then all the possibles coloured with X are true and can be forced - and all those with Y are false and can be eliminated. If we can prove that Y is true then vice-versa.
Everything is consistent up to this point, but the next conjugate causes problems. | Code: | | c3: 1e conjugates 1g |
1g in r5c3 is already coloured 1X and so we may colour the 1e in r4c3 with its conjugate colour 1Y.
This makes the coding in cell r3c4 1Y4f9Y. Let's look at this carefully. If Y is false everywhere on the grid, then the cell has the certainty 4 from 4f. But if Y has the value true everywhere on the grid then the cell must have 1 and 9 both as certainties. Assuming that the puzzle is well-formed and has an unique solution then this is impossible, from which we conclude that Y must be false in r3c4 - and everywhere else on the grid and its conjugate X must be true everywhere on the grid.
This almost solves the whole grid, apart from just 5 no-brainer cells which we could have coloured had we wished.
It has taken us 30 coloured pen strokes to get this far and we haven't had to make any notes or erase any pencil marks. By any measure this is an easy solution to a tricky problem.
Actually it does follow your 2-possible colour reasoning but extends it with ease on one sheet to 4 colours - 1,2,4,9
I hope that now makes it clear - but I'd be delighted to hear of any better solution.
Regards
Andrew
Last edited by AMcK on Thu Sep 08, 2005 10:09 pm; edited 1 time in total |
|
| Back to top |
|
 |
| Nick70
| | Joined: 08 Jun 2005 | | Posts: 160 | | : | |
Items |
|
 Posted: Thu Sep 08, 2005 3:01 pm Post subject: Posted: Thu Sep 08, 2005 3:01 pm Post subject: |
 |
|
| AMcK wrote: | | It has taken us 30 coloured pen strokes to get this far and we haven't had to make any notes or erase any pencil marks. By any measure this is an easy solution to a tricky problem. |
I think I should add here the customary plea for Angus to add pencilmark coloring to Simple Sudoku  |
|
| Back to top |
|
 |
| AMcK
| | Joined: 07 Apr 2005 | | Posts: 89 | | : | | Location: Cambridge |
Items |
|
 Posted: Thu Sep 08, 2005 3:02 pm Post subject: Posted: Thu Sep 08, 2005 3:02 pm Post subject: |
 |
|
| Nick70 wrote: | | AMcK wrote: | | That's a neat use of simple colouring that I haven't used before. |
Come on, how can you say that? We have been using it since day 1. |
Thank you for your helpful contribution Nick. I didn't say you haven't been using it. I merely said that I hadn't been using it since day 1. I believe it's called a humble admission of a mistake. Perhaps you never have to do that. |
|
| Back to top |
|
 |
| AMcK
| | Joined: 07 Apr 2005 | | Posts: 89 | | : | | Location: Cambridge |
Items |
|
 Posted: Thu Sep 08, 2005 3:09 pm Post subject: Posted: Thu Sep 08, 2005 3:09 pm Post subject: |
 |
|
| Nick70 wrote: | | angusj wrote: | | Both puzzles 4 & 6 required only one use of simple colors as illustrated above |
Both Turbots btw  |
Would you care to reveal the 2 Turbots, please.
Regards
Andrew |
|
| Back to top |
|
 |
| angusj
Site Admin
 | | Joined: 18 Jun 2005 | | Posts: 406 | | : | |
Items |
|
 Posted: Thu Sep 08, 2005 9:23 pm Post subject: Posted: Thu Sep 08, 2005 9:23 pm Post subject: |
 |
|
| AMcK wrote: | | Would you care to reveal the 2 Turbots |
Yes, I missed it too, but it's here (I've unhighlighted the superfluously colored cell):
| Code: | *-----------*
|.B.|G..|...|
|...|..x|...|
|...|...|...|
|---+---+---|
|...|...|...|
|...|...|...|
|...|...|...|
|---+---+---|
|...|...|...|
|...|...|...|
|.G.|..B|...|
*-----------* |
|
|
| Back to top |
|
 |
| AMcK
| | Joined: 07 Apr 2005 | | Posts: 89 | | : | | Location: Cambridge |
Items |
|
 Posted: Thu Sep 08, 2005 10:06 pm Post subject: Posted: Thu Sep 08, 2005 10:06 pm Post subject: |
 |
|
| angusj wrote: | | AMcK wrote: | | Would you care to reveal the 2 Turbots |
Yes, I missed it too, but it's here (I've unhighlighted the superfluously colored cell):
| Code: | *-----------*
|.B.|G..|...|
|...|..x|...|
|...|...|...|
|---+---+---|
|...|...|...|
|...|...|...|
|...|...|...|
|---+---+---|
|...|...|...|
|...|...|...|
|.G.|..B|...|
*-----------* |
|
Excellent! So perhaps the simple colouring rule should be ...
For a given possible, if a suspect cell containing the possible lies in a house containing one element of a conjugate pair and lies also in another house containing the other element of the conjugate pair then the possible may be eliminated from the suspect cell. This definition covers row/column, row/box and column box instances. It doesn't matter whether the suspect cell is coloured or not - so long as it's not part of the intersecting conjugate pair.
Proof: One of the two elements of conjugate pair must be true. If the first element is true the it excludes the suspect cell in the first house. If the second element is true the it excludes the suspect cell in the second house. In either of the two cases, the possible is impossible in the suspect cell.
I don't believe this method was in either my initial April examples of colouring, Doug's June definition nor in Nick70's July "three techniques that can be used after coloring" post. But it's very useful and I'm sorry I didn't know about it earlier.
Regards, Andrew |
|
| Back to top |
|
 |
| Nick70
| | Joined: 08 Jun 2005 | | Posts: 160 | | : | |
Items |
|
 Posted: Thu Sep 08, 2005 10:21 pm Post subject: Posted: Thu Sep 08, 2005 10:21 pm Post subject: |
 |
|
| AMcK wrote: | | Nick70 wrote: | | AMcK wrote: | | That's a neat use of simple colouring that I haven't used before. |
Come on, how can you say that? We have been using it since day 1. |
Thank you for your helpful contribution Nick. I didn't say you haven't been using it. I merely said that I hadn't been using it since day 1. |
I said "we" as in both me and you. YOU have been using it before I did! |
|
| Back to top |
|
 |
| angusj
Site Admin
 | | Joined: 18 Jun 2005 | | Posts: 406 | | : | |
Items |
|
 Posted: Thu Sep 08, 2005 11:05 pm Post subject: Posted: Thu Sep 08, 2005 11:05 pm Post subject: |
 |
|
There are 3 ways to use Simple Coloring that I'm aware of:
1. Candidate grouped with both conjugate colors
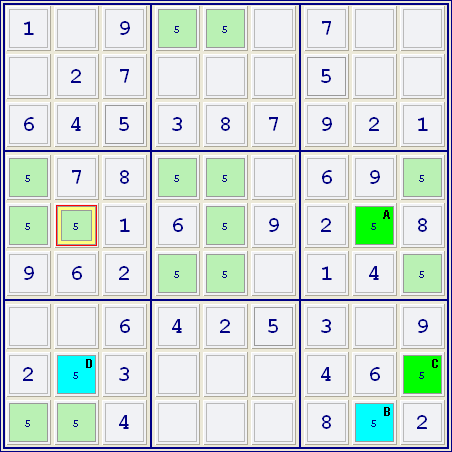
2. Cells with the same conjugate color sharing a group
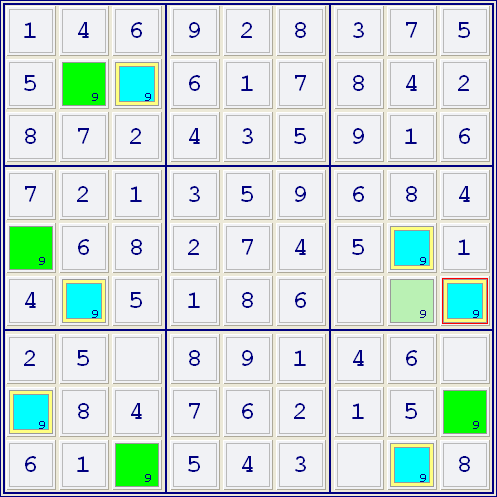
3. Candidates for an entire group also group with cells of the same conjugate color
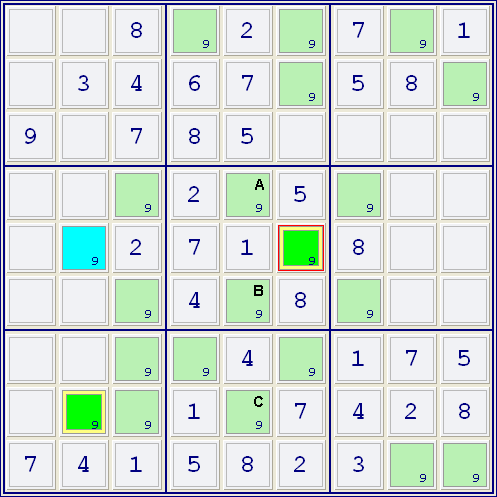
In each of these examples the candidate in the selected cells can be excluded. |
|
| Back to top |
|
 |
| Nick70
| | Joined: 08 Jun 2005 | | Posts: 160 | | : | |
Items |
|
 Posted: Thu Sep 08, 2005 11:25 pm Post subject: Posted: Thu Sep 08, 2005 11:25 pm Post subject: |
 |
|
| AMcK wrote: | | I don't believe this method was in either my initial April examples of colouring, Doug's June definition nor in Nick70's July "three techniques that can be used after coloring" post. |
Your post says:
| AMcK wrote: | In row 2
We have proved {2,1}=e and {2,6}=f are conjugate
We may now eliminate 1 from {2,2} |
This is exactly the same reasoning, the only difference being that the three cells are all in the same unit in this case, which isn't a requirement. But the logic is already there!
I now realise that in MY post I was also talking about a single unit. Frankly I can't remember if this was a mistake in the explanation, or a lack of understanding.
For sure in this other post, later in July, talking about "advanced" colouring, the mistake wasn't repeated:
| Nick70 wrote: | | b/ you prove that e.g. A+ ~ B+ and A- ~ B+. This means that B+ is false, thefore B- is true and you can promote the pencilmarks colored that way. |
Unfortunately there's still a slight (and new!) mistake there, in assuming that the excluded possible has a conjugate.
The final description of "supercolouring", at last is free of those mistakes and omissions. |
|
| Back to top |
|
 |
| Nick70
| | Joined: 08 Jun 2005 | | Posts: 160 | | : | |
Items |
|
 Posted: Fri Sep 09, 2005 9:31 am Post subject: Posted: Fri Sep 09, 2005 9:31 am Post subject: |
 |
|
I should add that AngusJ's site has been showing an example of this for several weeks.
Not to mention the Turbot fish description. |
|
| Back to top |
|
 |
| AMcK
| | Joined: 07 Apr 2005 | | Posts: 89 | | : | | Location: Cambridge |
Items |
|
 Posted: Fri Sep 09, 2005 3:03 pm Post subject: Posted: Fri Sep 09, 2005 3:03 pm Post subject: |
 |
|
| Nick70 wrote: | | The final description of "supercolouring", at last is free of those mistakes and omissions. |
Good, so we're all agreed. I think that it is important to develop human usable sub-heuristics from the powerful computer-friendly algorithms we are developing. In this sense, Angus's multi-house exclusion is a neat addition to simple colouring (I've almost got it working). I also feel that my simple solution of Ultra 2, using your "advanced coloring" subset, is a usable technique.
Regards
Andrew |
|
| Back to top |
|
 |
| angusj
Site Admin
 | | Joined: 18 Jun 2005 | | Posts: 406 | | : | |
Items |
|
 Posted: Fri Sep 09, 2005 11:00 pm Post subject: Posted: Fri Sep 09, 2005 11:00 pm Post subject: |
 |
|
| AMcK wrote: | | In this sense, Angus's multi-house exclusion is a neat addition to simple colouring |
Just in case I've given the impression that it's 'my' addition to colours - it was Ocean ( http://www.sudoku.com/forums/viewtopic.php?p=7954#7954 ) who first spotted that one. |
|
| Back to top |
|
 |
|






