
|
| View previous topic :: View next topic |
| Author |
Message |
| Bob Hanson
| | Joined: 05 Oct 2005 | | Posts: 187 | | : | | Location: St. Olaf College |
Items |
|
 Posted: Thu Oct 13, 2005 4:48 am Post subject: 3D deconstruction of 9x9 Sudoku provides key to rules Posted: Thu Oct 13, 2005 4:48 am Post subject: 3D deconstruction of 9x9 Sudoku provides key to rules |
 |
|
[This message refers to standard 9x9 Sudoku, not some sort of 3D analog.]
I have been studying the page developing out of ATT Research at
http://www.research.att.com/~gsf/sudoku/
This is really fascinating. This page attempts to classify constraints into different subclasses, namely "X", "Y", and "W", among others.
I wonder if anyone else has noticed that what this page refers to as "X-constraints" and "Y-constraints" are simply two different projections of a 3D deconstruction of 9x9 Sudoku, where each candidate number is on its own plane, stacked "vertically" above the plane of the board.
See, for example, the interactive 3D model of Sudoku at http://www.stolaf.edu/people/hansonr/sudoku.
Thus, while "X-constraints" focus on a specific candidate number (horizontal slice of a given color on the 3D deconstruction), Y constraints simply extend this to the vertical dimension, where we envision each candidate possibility to be on its own plane.
This suggests no fundamental distinction between "X" and "Y" constraints. Indeed, if one treats a "verticallizing" cell of the Y-constraint examples as a vertical strong edge of a standard cycle, then all rules relating to "X" constraints apply to Y constraints. (Which means, of course, that there are several more subclass examples of Y-constraints.)
Similarly, "W" constraints along with certain X-constraints are simply subset elimination (generally considered ONLY in a vertical sense) done horizontally. Or, to put it another way, allowing X and W constraints to act vertically we have subset elimination.
Thus:
A) "X-constraints" are simply a subset of "Y-constraints."
B) Certain "subset eliminations" and "X- or W-constraints" are one in the same, done in different planes. (hidden pairs and naked pairs are simply two different orientations of Xwings; hidden/naked triples are simply two different orientations of swordfish, etc.).
What I don't quite understand is why people are focusing on "cycles". Yes, cycles are created, but the essential characteristic of a "strong edge" is not that it makes a cycle, but that it determines a "parity" for a subset of the board. An alternating "grid" of points is produced which may or may not be cyclic. It really doesn't matter. When this parity check delivers a logical inconsistency due to an incompatibility with another parity check from another source on the board, we have an elimination. (To be fair, that "form another source" involves a cycle.)
Except for the fact that a weak edge is necessary to separate two "ends" of a strong chain in a particular row, cell, or block, there seems to me no need to focus on them. Thus, for example, Rules X1 and X3 simply state the same thing -- that any cell of a given candidate possibility k being acted upon by two cells of opposite parity must be eliminated. (Because one or the other must then be true.) In the one case we have a weak edge because the cell is in the same column as the two ends of the strong sequence; in the other it is in a column and a block. I guess I don't see the point of making that distinction -- a dependency, whether row, column, block, or cell is just the same fundamentally. This is precisely the principle in the discussion for Y constraints, of course.
At the above web page I show how all this cycle business can be dispensed with. -- at least programmatically. So, for example, noncyclic "W constraints" are the basis for all subset elimination carried out by this web application code.
Please don't get me wrong. The cyclic analysis is brilliant and clear. I think in terms of human solving, the cycle business is a nice trick. I just hope people aren't trying to figure out all the ways to generate all the possible cycles, or to think that you have to find the cycles to solve a Sudoku, although in some cases I guess this could be valuable. Maybe all I'm saying is what everyone already knows: that the cycle analysis is just a shorthand for what I think people call "coloring". (But I'm unclear about that.)
_________________
Bob Hanson
Professor of Chemistry
St. Olaf College
Northfield, MN
http://www.stolaf.edu/people/hansonr |
|
| Back to top |
|
 |
| Lummox JR
| | Joined: 07 Sep 2005 | | Posts: 202 | | : | |
Items |
|
 Posted: Thu Oct 13, 2005 5:47 am Post subject: Re: 3D deconstruction of 9x9 Sudoku provides key to rules Posted: Thu Oct 13, 2005 5:47 am Post subject: Re: 3D deconstruction of 9x9 Sudoku provides key to rules |
 |
|
| Bob Hanson wrote: | Thus, while "X-constraints" focus on a specific candidate number (horizontal slice of a given color on the 3D deconstruction), Y constraints simply extend this to the vertical dimension, where we envision each candidate possibility to be on its own plane.
This suggests no fundamental distinction between "X" and "Y" constraints. Indeed, if one treats a "verticallizing" cell of the Y-constraint examples as a vertical strong edge of a standard cycle, then all rules relating to "X" constraints apply to Y constraints. (Which means, of course, that there are several more subclass examples of Y-constraints.) |
I too have found the cube representation to be quite interesting. When first considering the grid as a cube of possibilities, I finally realized how supercoloring works. Supercoloring just takes the same method of finding conjugates that regular coloring uses, but extends it across all the digits. By figuring out which colors are mutually exclusive, you can look for 1) colors that exclude themselves and are therefore false, or 2) intersections between their conjugates.
I haven't checked out that page, but presumably the box constraint is also in there. If you take the 9x9x9 cube and slice it in a non-digit direction, you get a column-digit set or a row-digit set, and if you slice out a 3x3x9 chunk you get a box-digit set, which works out as a 9x9 plane if you "unroll" it.
| Quote: | | B) Certain "subset eliminations" and "X- or W-constraints" are one in the same, done in different planes. (hidden pairs and naked pairs are simply two different orientations of Xwings; hidden/naked triples are simply two different orientations of swordfish, etc.). |
Yep, that's one of the more interesting facets of subsets. Just like a naked subset has a hidden equivalent, there's also the fact that a swordfish by columns has an X-wing or swordfish (or more) by rows.
| Quote: | | What I don't quite understand is why people are focusing on "cycles". Yes, cycles are created, but the essential characteristic of a "strong edge" is not that it makes a cycle, but that it determines a "parity" for a subset of the board. An alternating "grid" of points is produced which may or may not be cyclic. It really doesn't matter. When this parity check delivers a logical inconsistency due to an incompatibility with another parity check from another source on the board, we have an elimination. (To be fair, that "form another source" involves a cycle.) |
"Parity" is definitely an interesting way to look at it, although it might be too simple a concept to be very useful. What you've just described sounds like simple coloring when done with just one pair of colors. Specifically it sounds like the test in which one color is eliminated because it occurs twice in the same house.
| Quote: | | Except for the fact that a weak edge is necessary to separate two "ends" of a strong chain in a particular row, cell, or block, there seems to me no need to focus on them. Thus, for example, Rules X1 and X3 simply state the same thing -- that any cell of a given candidate possibility k being acted upon by two cells of opposite parity must be eliminated. (Because one or the other must then be true.) In the one case we have a weak edge because the cell is in the same column as the two ends of the strong sequence; in the other it is in a column and a block. I guess I don't see the point of making that distinction -- a dependency, whether row, column, block, or cell is just the same fundamentally. This is precisely the principle in the discussion for Y constraints, of course. |
You've just described another method of elimination by simple coloring, again when using only one pair of colors. Of course coloring is actually a lot more powerful if you use complete coloring with multiple color sets; it can find for example that two choices cannot both be true, so at least one of their conjugates must be true; this allows for that same style of elimination you just mentioned.
| Quote: | At the above web page I show how all this cycle business can be dispensed with. -- at least programmatically. So, for example, noncyclic "W constraints" are the basis for all subset elimination carried out by this web application code.
Please don't get me wrong. The cyclic analysis is brilliant and clear. I think in terms of human solving, the cycle business is a nice trick. I just hope people aren't trying to figure out all the ways to generate all the possible cycles, or to think that you have to find the cycles to solve a Sudoku, although in some cases I guess this could be valuable. Maybe all I'm saying is what everyone already knows: that the cycle analysis is just a shorthand for what I think people call "coloring". (But I'm unclear about that.) |
It sounds like a shorthand for an ultrasimplified form of coloring, yes. Of course "shorthand" may be a misnomer. Coloring is pretty clear-cut, but this sounds like it's "over-mathing" an otherwise simple concept, and with poorer results since it's only equivalent to partial coloring.
...Or perhaps, partial supercoloring as well. While I've long known you can reformat any one of those constraints into a 9x9 grid and perform coloring on that, it's probably unlikely to catch much. The work involved in re-representing the grid 27 times could just as easily be put toward supercoloring. Typically in supercoloring I've found that the kinds of eliminations that this sort of "house coloring" would find would be rare, and that only makes sense because it takes away the box constraint as a valuable tool. Usually if simple coloring fails, supercoloring needs the entire grid to come up with anything useful. |
|
| Back to top |
|
 |
| dukuso
| | Joined: 14 Jul 2005 | | Posts: 424 | | : | | Location: germany |
Items |
|
 Posted: Thu Oct 13, 2005 7:01 am Post subject: Posted: Thu Oct 13, 2005 7:01 am Post subject: |
 |
|
(the link doesn't work for me]
don't we get these symmetries gratis with the exact-cover method
("dancing links, DLX) ?
So, when you try to formulate swordfish etc. in binary-matrix-
speak, you should get the symmetric rules automatically.
(I haven't tried, don't even know what swordfish is) |
|
| Back to top |
|
 |
| Lummox JR
| | Joined: 07 Sep 2005 | | Posts: 202 | | : | |
Items |
|
 Posted: Thu Oct 13, 2005 6:32 pm Post subject: Posted: Thu Oct 13, 2005 6:32 pm Post subject: |
 |
|
The exact-cover matrix actually operates a bit differently than the 9x9x9 cube. For example, you can use this rule in DLX which is an equivalent to pointing pairs or box-line intersections, but applies to all exact-cover problems:
If all of the choices for constraint A also satisfy constraint B, all other choices that satisfy B can be eliminated.
Swordfish is best understood in the context of a binary grid, and finding subsets. To find a naked or hidden triple, you'd slice the cube in a different direction or take a box section and get a different 9x9. If you sliced the cube so that the columns of the 9x9 grid are digits, and the rows are the positions in a house that they can occupy, a hidden triple appears where in 3 columns of the grid, the only possible choices occupy only 3 rows. Similarly a naked triple finds 3 rows whose only possibilities occupy the same 3 columns. Swordfish is identical to this except it slices the cube into a single digit 9x9 grid where the columns and rows are the actual columns and rows of the puzzle. A swordfish can be found by either columns or rows. X-wing works the same way, but it only finds a pair of columns/rows rather than 3 or more of them. |
|
| Back to top |
|
 |
| gsf
| | Joined: 18 Aug 2005 | | Posts: 411 | | : | | Location: NJ USA |
Items |
|
 Posted: Thu Oct 13, 2005 10:05 pm Post subject: Re: 3D deconstruction of 9x9 Sudoku provides key to rules Posted: Thu Oct 13, 2005 10:05 pm Post subject: Re: 3D deconstruction of 9x9 Sudoku provides key to rules |
 |
|
| Bob Hanson wrote: |
I have been studying the page developing out of ATT Research at
http://www.research.att.com/~gsf/sudoku/
What I don't quite understand is why people are focusing on "cycles". Yes, cycles are created, but the essential characteristic of a "strong edge" is not that it makes a cycle, but that it determines a "parity" for a subset of the board. An alternating "grid" of points is produced which may or may not be cyclic. It really doesn't matter. When this parity check delivers a logical inconsistency due to an incompatibility with another parity check from another source on the board, we have an elimination. (To be fair, that "form another source" involves a cycle.)
|
(X-cycle from X-wing on single candidates, Y-cycle from XY-wing on naked pairs)
Forced values or candidate elimination are not possible until the strong/weak edge chain closes on itself (and makes a cycle.) All of the action takes place at the weak edges of the cycle. The parity of the cycle segments (even or odd edge count) determines the actions that can be taken.
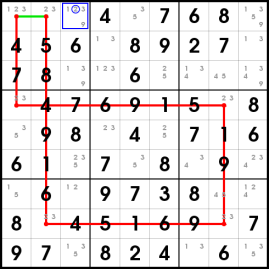
This puzzle illustrates the 3 X cycle types:
| Code: |
. . . | 4 . 7 | 6 8 .
4 5 6 | . 8 9 | 2 7 .
7 8 . | . 6 . | . . .
---------------------
. 4 7 | 6 9 1 | 5 . 8
. 9 8 | . . . | 7 . 6
6 . . | 7 . 8 | . 9 .
---------------------
. 6 . | 9 7 3 | 8 . .
8 . 4 | 5 1 6 | 9 . 7
9 7 . | 8 2 4 | . 6 .
|
This type 1 X cycle on candidate 2 allows the weak edge candidates not participating in the cycle to be eliminated (strong edges red, weak edges green, candidate eliminations blue):
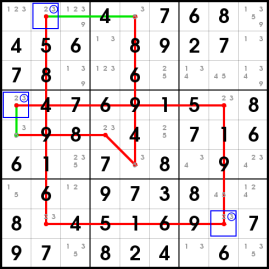
This type 2 X cycle on candidate 3 allows the endpoints (and alternating inner points) of the even strong segement to be eliminated:
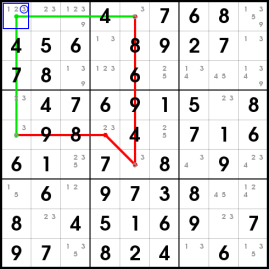
This type 3 X cycle on candidate 3 allows the midpoint of the even weak segement to be eliminated:
I think you misinterpreted the Y cycle description (or I was too terse). X and Y cycle edges are not equivalent. X cycle edges are between cells with a single candidate value. Y cycle edges are between naked pair cells with (at least) one candidate value in common.
Also, I realize that there must be a relationship between the X and Y cycles and the various forms of coloring and tabling etc. I've posted some annotated puzzles in
http://www.research.att.com/~gsf/sudoku/taxonomy.dat
where each line of puzzle data is preceded by a "..." annotation line that lists the constraint method used to solve the puzzle. 1-constrained or 2-constrained means that my solver had to backtrack to solve. It would be interesting to correlate these with the solution methods used by the other solvers. |
|
| Back to top |
|
 |
| dukuso
| | Joined: 14 Jul 2005 | | Posts: 424 | | : | | Location: germany |
Items |
|
 Posted: Fri Oct 14, 2005 3:59 am Post subject: Posted: Fri Oct 14, 2005 3:59 am Post subject: |
 |
|
>The exact-cover matrix actually operates a bit differently than
>the 9x9x9 cube.
>For example, you can use this rule in DLX which
>is an equivalent to pointing pairs or box-line intersections,
>but applies to all exact-cover problems:
>
>If all of the choices for constraint A also satisfy constraint B,
>all other choices that satisfy B can be eliminated.
(B=A|B)==>B=A
you see, how easy it is formulated with exact-cover-speak ?
you could even use A<=B for B=A|B ("|" for "or" as in C)
>Swordfish is best understood in the context of a binary grid,
>and finding subsets. To find a naked or hidden triple,
>you'd slice the cube in a different direction or take
>a box section and get a different 9x9. If you sliced
>the cube so that the columns of the 9x9 grid are digits,
>and the rows are the positions in a house that they can
>occupy, a hidden triple appears where in 3 columns of the grid,
>the only possible choices occupy only 3 rows. Similarly a naked
>triple finds 3 rows whose only possibilities occupy the same 3
>columns. Swordfish is identical to this except it slices the
>cube into a single digit 9x9 grid where the columns and rows
>are the actual columns and rows of the puzzle. A swordfish
>can be found by either columns or rows. X-wing works the
>same way, but it only finds a pair of columns/rows rather
>than 3 or more of them.
since in exact-cover the constraints are only listed and not
distinguished you needn't slice the cube into different
directions. (rotate) Once you formulated it for one
"direction" you have it for all the others.
"choose the cell with fewest candidates"
would be in exact-cover : "choose the column(=constraint)
with fewest ones(=satisfying placements).
This would not only include cells with fewest candidates
but also e.g. symbols with fewest possible positions in a block etc.
Or did I misunderstand the cube and we have the possible
candidates for a cell as 3rd coordinate ? |
|
| Back to top |
|
 |
| Lummox JR
| | Joined: 07 Sep 2005 | | Posts: 202 | | : | |
Items |
|
 Posted: Fri Oct 14, 2005 4:25 am Post subject: Posted: Fri Oct 14, 2005 4:25 am Post subject: |
 |
|
| dukuso wrote: | >If all of the choices for constraint A also satisfy constraint B,
all other choices that satisfy B can be eliminated.
(B=A|B)==>B=A
you see, how easy it is formulated with exact-cover-speak ?
you could even use A<=B for B=A|B ("|" for "or" as in C) |
That's one way to do it. I'm sure with set notation and logical operators it could look even neater mathematically.
| Quote: | since in exact-cover the constraints are only listed and not
distinguished you needn't slice the cube into different
directions. (rotate) Once you formulated it for one
"direction" you have it for all the others.
"choose the cell with fewest candidates"
would be in exact-cover : "choose the column(=constraint)
with fewest ones(=satisfying placements).
This would not only include cells with fewest candidates
but also e.g. symbols with fewest possible positions in a block etc.
Or did I misunderstand the cube and we have the possible
candidates for a cell as 3rd coordinate ? |
Yep, you did. The cube is a 9x9x9 matrix of truth values: Yes, no, maybe. It's the maybes that concern us.
I'm not really sure finding subsets via exact cover is possible. You have to be selective in which columns you pick, and then you have to reformulate the rows so they all "line up" in a 9x9 grid. Once you have such a grid (which could be represented in many ways, including by bit flags), you can use any subset algorithm you like. Using the DLX matrix directly for subsets, though, shouldn't be doable due to its construction. |
|
| Back to top |
|
 |
| dukuso
| | Joined: 14 Jul 2005 | | Posts: 424 | | : | | Location: germany |
Items |
|
 Posted: Fri Oct 14, 2005 12:16 pm Post subject: Posted: Fri Oct 14, 2005 12:16 pm Post subject: |
 |
|
here is my attempt to describe subsets (naked or hidden,
that's the same here) in exact-cover-speak.
In fact, it's even more general but for sudoku it would
probably essentially reduce to naked/hidden subsets.
I pretend, that probably most constraint programming
with alldifferent can be done more nicely in exact-cover-speak,
but I couldn't find whether anybody had already tried this.
I had email with W.vanHoeve, he wrote a large online-survey
about alldifferent constraints, but wasn't even aware that these
can be transformed into exact-cover problems, nor had he
any reference for this.
I'd really like to know, whether this sort of formulation has been
described elsewhere.
----------Definitions:
exact-cover problem:
given a binary n*m matrix A with n rows and m columns,
find a subset S of the rows which sums to the all-1-vector.
Row r is adjacent to column c, iff A(r,c)=1
("placement r satisfies constraint c").
Let _S be the set of all solutions.
Two rows(columns) are called adjacent, iff there exists a column(row)
to which they both are adjacent.
For a set D of columns(rows) let N(D) be the set of all rows(columns)
adjacent to any column(row) in D.
The exact-cover problem is being solved by recursively selecting some
row r, deleting columns N({r}) and rows N(N({r}) and thus
reducing it to a smaller exact-cover problem called E(A,r).
Just deleting row r without any other changes gives problem E(r)
For any column c, the exact-cover-problem A has a solution S,
iff there exists r in N(c), r in S such that the reduced exact-cover problem
E(A,r) has the solution S-{r}.
---------------subsets-theorem :
Let D be a set of k different,mutually nonadjacent columns.
Assume N(D) partitions into k disjoint sets R1,..,Rk
each consisting of mutually adjacent rows.
If r is a row not in N(D) but adjacent to all rows in R1 then
_S=_S(E(r)) , so r can be deleted.
proof:
This is because placement r would delete all of R1 but none of D.
Any subsequent placement q in Ri deletes all of Ri and one of D,
so one in D would be left without adjacent rows.
In case of sudokus,the Ri would typically be given as subsets
of neighbor-sets of some columns ci adjacent to D. Ri<=N(ci).
example: (r:row,c:column,s:symbol, "851" is short for r8c5s1)
suppose after some placements block 8 has these candidate-sets:
| Code: |
r7c4:{4,5,6,9} r7c5:{4,9} r7c6:{5,6,9}
r8c4:{2,4} r8c5:{1,2,3,4,7} r8c6:{1,2,3,7}
r9c4:{2,5,6} r9c5:{1,2,7} r9c6:{8}
|
we have D={b8s1,b8s3,b8s7},k=3,N(D)={851,853,857,861,863,867,961,967}
R1={851,853,857}
R2={861,863,867}
R3={961,967}
r=854, N(r)>=R1, r not in N(D), so r can be deleted
"hidden triple in block 8 for symbols 1,3,7"
extract of the exact-cover-matrix: ("o": 1 "." : 0 )
| Code: |
|r8c5 r8c6 r9c6 {b8s1,b8s3,b8s7}=D
---+--------------------------------
851| o . . o . .
853| o . . . o .
857| o . . . . o
861| . o . o . .
863| . o . . o .
867| . o . . . o
961| . . o o . .
967| . . o . . o
854| o . . . . .
---------------
sum ? ? ? 3 2 3
|
Last edited by dukuso on Fri Oct 14, 2005 6:12 pm; edited 7 times in total |
|
| Back to top |
|
 |
| Bob Hanson
| | Joined: 05 Oct 2005 | | Posts: 187 | | : | | Location: St. Olaf College |
Items |
|
 Posted: Fri Oct 14, 2005 3:09 pm Post subject: Posted: Fri Oct 14, 2005 3:09 pm Post subject: |
 |
|
Thank you all for contributing here. I see now that I had mistakenly read that description of Y-constraints -- I could suggest some alternative wording that does not include the issue of "exactly two in a given row/column/block". This I think is what threw me off.
Continued success in Sudoku Assistant: http://www.stolaf.edu/people/hansonr/sudoku
This morning I realized that X and Y constraints are indeed simply two flavors of the same thing -- one operating in the plane of the board (X) and one operating perpendicular to it (Y). (Thus, Glenn's Y-constraint entry into a cell with two values {a,b} via {a} and leaving via {b} amounts to the equivalent of THREE X-constraint-like edges, where the a--b switch is one strong edge. (Exactly like a strong naked pair edge in a row/column/block in the case an X-constraint.)
I think I've successfully implemented those now with no "cycle" aspect (at least programmatically), just parity. With one caveate -- I'm not checking for weak links between independent chains the way Glenn Fowler describes. (One odd sequence with weak links to n even sequences....) That amounts to phasing the independent chains so that they contribute to a whole. (Or, just bridging the chains....oh, funny.... sure....I see...too easy! Oh, my!)
I think the connection to multicoloring probably relates to what I am going to say next:
I would like to call my chain-strategy "M" for Medusa. Rather than thinking of cycles, I suggest thinking of the problem in relation to a network of snakes, similar to Medusa's head.
http://www.class.uidaho.edu/mckeever/images/caravaggio_Head%20of%20Medusa.GIF
As these snakely chains wind their way through the 3D cube, they pick up dependencies all over the place -- in every row, column, and block they pass through. The X- and Y- constraint business simply capitalizes on this.
A general "M" strategy would merge these two separate "X" and "Y" labyrinths into one.
A generalization to triples would I suppose take me fully into the world of multicoloring. For example, one could start a binary chain with a triple and see where it leads. A 3-point Medusa search would show up incompatibilities between alternative pairings and perhaps disallow one of them. (Note: still just two colors, I think. Maybe not, though?)
I'll admit to (a) not being a mathematician and (b) working too fast for my own good here. Thanks in advance.
Enjoy.
_________________
Bob Hanson
Professor of Chemistry
St. Olaf College
Northfield, MN
http://www.stolaf.edu/people/hansonr |
|
| Back to top |
|
 |
|
|
You cannot post new topics in this forum
You cannot reply to topics in this forum
You cannot edit your posts in this forum
You cannot delete your posts in this forum
You cannot vote in polls in this forum
|

Powered by phpBB © 2001, 2005 phpBB Group
Igloo Theme Version 1.0 :: Created By: Andrew Charron |






