
|
| View previous topic :: View next topic |
| Author |
Message |
| Bob Hanson
| | Joined: 05 Oct 2005 | | Posts: 187 | | : | | Location: St. Olaf College |
Items |
|
 Posted: Thu Dec 22, 2005 2:14 pm Post subject: 729x324 exact cover 3D and S-DLX proposal Posted: Thu Dec 22, 2005 2:14 pm Post subject: 729x324 exact cover 3D and S-DLX proposal |
 |
|
In this posting I offer two suggestions:
1) A new 3D way of looking at the exact cover "matrix"
2) A possible optimization of DLX for Sudoku -- S-DLX
1) A new 3D way of looking at the exact cover "matrix"
----------------------------------------------------------------
It occurred to me after reading Knuth's paper again and writing
http://www.stolaf.edu/people/hansonr/sudoku/exactcover.htm that:
a) There's a heck of a lot wasted white space here
b) Sudoku isn't pentominos. All the pieces are identical
c) The DLX algorithm, though proposed for solving exact cover
problems, which are generally expressed in terms of a 2D matrix,
really doesn't require this. It's just a set of multiply linked nodes that,
hen depicted this way actually look pretty messy.
d) Knuth wasn't thinking Sudoku -- he was being far more general. He
proposes a single optimization strategy -- "start with 2-valued constraints"
-- but doesn't consider puzzle-specific optimizations.
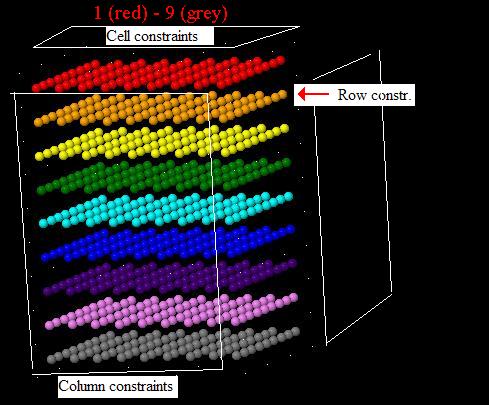
OK, so putting 2 and 2 together.... Consider the basic 729x324 matrix:
| Code: |
................................................................................................................
cell constraints (only one of value in each of 81 cells)------------------------- row constraints......
0 1 2 3 4 5 6 7 8 1 2 ...
123456789012345678901234567890123456789012345678901234567890123456789012345678901 123456789123456789...
cand/N 999999999999999999999999999999999999999999999999999999999999999999999999999999999 999999999999999999...
r1c1#1 1 |1 ...
r1c1#2 2 | 2 ...
r1c1#3 3 | 3 ...
r1c1#4 4 | 4 ...
r1c1#5 5 | 5 ...
r1c1#6 6 | 6 ...
r1c1#7 7 | 7 ...
r1c1#8 8 | 8 ...
r1c1#9 9 | 9 ...
-----------------------------------------------------------------------------------------------------------...
r1c2#1 1 |1 ...
r1c2#2 2 | 2 ...
r1c2#3 3 | 3 ...
r1c2#4 4 | 4 ...
r1c2#5 5 | 5 ...
r1c2#6 6 | 6 ...
r1c2#7 7 | 7 ...
r1c2#8 8 | 8 ...
r1c2#9 9 | 9 ...
-----------------------------------------------------------------------------------------------------------...
r1c3#1 1 |1 ...
r1c3#2 2 | 2 ...
...
...
...
|
Now, this matrix is not actually represented in any real DLX algorithm.
All it is is for the reader's benefit. The true data structure is a set of
nodes and links. So, I say, why not reorganize those links to suit
Sudoku?
a) Stack all the #1, #2, #3, ..., #9 lines on top of each other for a
given cell. Now we have 81 lines, each stacked 9 high.
b) Realign the lines by row, interlacing the columns. Now we have a
set of four 9x9x9 cube of "lines"
Surely a mess! But consider this: The line "markers" themselves,
r1c1#1, r1c2#2, etc.... form a 9x9x9 grid, like this:

But that's not all. So do each of the four column sets.
In fact, they all line up. In fact, we could just consider each of these
little "atoms" to be four nodes -- each dot represents all four nodes of the
exact cover matrix line that corresponds to that row, column, and value.
Now, the key to the exact cover business is keeping track of the number
of nodes in an exact cover matrix column -- the number of "competing
candidates." What about this line of information?
Well,  , it becomes a set of planes! A set of PROJECTIONS. , it becomes a set of planes! A set of PROJECTIONS.
Something like this:
Ah, that works for three of the four, anyway -- what about the blocks?
Well, that's special to Sudoku, of course, as well. I suggest we just
stack the numbers in the bottom right-and corner of each block --
nine stacks of nine digits. OK, it's not ideal. But it works.
(Oh, and by the way, all the 3D Medusa "strong chains" are now marked
with "2"s in these reorganized constraint lists.)
So, that's my "new" way of looking at the 729x324 matrix:
Each point in a single 9x9x9 cube represents one line in the exact cover matrix.
Each point involves four linked list nodes packed into one convenient location.
Three of the four 81-member sets of "constraint column headers" is a
projection onto a 9x9 plane -- a "face" of this cube.
The fourth 81-member header set, for "one of each digit per block," is
simply distributed in 9 stacks of 9 digits, associated with each block in
some convenient way.
2) A possible optimization of DLX for Sudoku -- S-DLX
--------------------------------------------------------------
Now, I think it should be clear what the DLX algorithm does. It "covers"
all matrix-column/row combinations sequentially in all possible combinations
and checks each time to see if there is an "exact cover" -- exactly one
node in each constraint column.
In Sudoku, this corresponds to sequentially eliminating each possibility
-- each "mark" on a marked Sudoku -- and (blindly) seeing if, by chance,
we have a solution.
Delete every possible combination of marks -- find every possible solution.
That's DLX. Knuth's point in the Dancing Links paper is simply that
there is a fast way to do this -- by delinking and relinking nodes.
In a 3D sense, it means taking out these atoms -- these dots -- one by
one and seeing if there are still any Sudoku columns, rows, or blocks that
have more than one "dot" in them. And, if an impossibility arises, putting
that dot back in and trying another.
DLX thus uses what is called "depth first" backtracking.
The DLX routine is a brute-force technique, pure backtracking, that is
efficient simply because it works solely with linked lists.
So, Knuth in his Dancing Links paper points out that without some additional
idea, this is REALLY inefficient. His solution was to start always by
deleting a node from the constraint having the smallest number of
competitors. (That is, always start testing with the strong chains.)
What I say next may not work. It's simply a proposal. I don't have the
capability here to test it out, so take this for what it is: just a hypothesis.
Obviously, what you have to do at the beginning of any Sudoku DLX
analysis is account for all the clues. This is done by unlinking all the
nodes associated with all the clues and removing all four nodes from
any competing candidate.
I believe that in easy Sudoku puzzles this actually solves the puzzle -- the
DLX algorithm never even needs recursing.
The next step, then, is to start the DLX going. I suggest that Knuth's
starting optimization amounts essentially to "trial and error starting
with the strong chains."
Now, here's my suggestion: Do a little more work up front to add some
more linked lists, and do a SET OF DIFFERENT, MUCH SMALLER exact
cover DLX searches first.
The idea is that because Sudoku has this specific type of exact-cover
3D nature, there is more information there that could be in linked lists.
Basically, what our "setting the clues" business does is recognize only
the very simplest of NxN grids -- singlets. If we had added plane-by-plane
links to our "atoms" we could have done something a bit more
sophisticated and interesting. Setting the links can't possibly take that
much time.
If we had, say, considered "just Row 1" we might have noticed a
naked pair. Any human solver would treat this like a "grouped single"
and done the same sort of starting elimination that setting up the DLX
does.
So, why not look for naked pairs -- X-wings in another dimension --
before starting DLX? And, for that matter, why not use DLX to do it?
After all, what a swordfish is is a 3x3 exact cover in a particular plane.
What a naked triple is is a 3x3 exact cover in a different plane. These
exact covers can be looked for recursively using DLX. A "solution" in
that case is a "find" of an X-wing, a hidden triple, a swordfish, etc.
All one would need to do is to add a few more linked lists.
The benefit is that the DLX routine then only has to work with a far smaller
subset of the information, because more "clues" have been found initially.
I suggest "S-DLX" for this method, and though I can't test it myself,
I suggest this could radically improve a Sudoku DLX solver's speed.
_________________
Bob Hanson
Professor of Chemistry
St. Olaf College
Northfield, MN
http://www.stolaf.edu/people/hansonr |
|
| Back to top |
|
 |
| dukuso
| | Joined: 14 Jul 2005 | | Posts: 424 | | : | | Location: germany |
Items |
|
 Posted: Fri Dec 23, 2005 9:11 am Post subject: Posted: Fri Dec 23, 2005 9:11 am Post subject: |
 |
|
I'm afraid most of your sudoku-specific ideas to "improve"
the DLX are not efficient, i.e. will not speed up the search.
While those ideas which do result in faster solving
are not sudoku-specific and work e.g. for QWH as well. |
|
| Back to top |
|
 |
| gsf
| | Joined: 18 Aug 2005 | | Posts: 411 | | : | | Location: NJ USA |
Items |
|
 Posted: Fri Dec 23, 2005 3:29 pm Post subject: Posted: Fri Dec 23, 2005 3:29 pm Post subject: |
 |
|
9x9 sudoku may be too simple to expose the combinatorial explosion of higher order problems. As problem size increases so do the number of backtrack nodes, and then the per node computations overwhelm everything else. This is where techniques like forward checking and arc consistency come into play. They attempt to efficiently reduce the number of backtrack nodes by using the backtrack tree itself to flush out physical properties rather than computing those properties directly. For example, a simple one level forward check handles naked pairs without backtracking and provides the info needed to pick the best candidate(s) to backtrack on.
I don't use dancing links. For 9x9 sudoku how many link operations are required to assign a value to a cell and then retract that assignment? Are any other computations required along with the retraction? |
|
| Back to top |
|
 |
| dukuso
| | Joined: 14 Jul 2005 | | Posts: 424 | | : | | Location: germany |
Items |
|
 Posted: Fri Dec 23, 2005 3:44 pm Post subject: Posted: Fri Dec 23, 2005 3:44 pm Post subject: |
 |
|
I have about 500 placements per millisecond, that's
about 1000 CPU-cycles per placement, including search for
the best constraint, updating all the counts of neighbors,
deleting (marking as used) rows and columns, and later
un-placement when backtracking |
|
| Back to top |
|
 |
| gsf
| | Joined: 18 Aug 2005 | | Posts: 411 | | : | | Location: NJ USA |
Items |
|
 Posted: Fri Dec 23, 2005 3:55 pm Post subject: Posted: Fri Dec 23, 2005 3:55 pm Post subject: |
 |
|
| After posing that question I realized almost any answer will be apples to oranges. The candidate selection strategy and other backtrack optimizations will skew per-node costs beyond comparison. For instance, despite claiming that per-node computations should be kept to a minimum, my solver only has 5 backtrack nodes for the top1465 9x9 sudoku, so my cycles per node are way up there. |
|
| Back to top |
|
 |
|
|
You cannot post new topics in this forum
You cannot reply to topics in this forum
You cannot edit your posts in this forum
You cannot delete your posts in this forum
You cannot vote in polls in this forum
|

Powered by phpBB © 2001, 2005 phpBB Group
Igloo Theme Version 1.0 :: Created By: Andrew Charron |





