
|
| View previous topic :: View next topic |
| Author |
Message |
| dobrichev
| | Joined: 18 Dec 2009 | | Posts: 28 | | : | |
Items |
|
 Posted: Thu Mar 25, 2010 8:53 pm Post subject: More data Posted: Thu Mar 25, 2010 8:53 pm Post subject: More data |
 |
|
Here is the status at the moment
New data
Data for the known 37 and 38-clue solution grids are available.
The updated raw data for the following graphics are in these files:
The islands
Each Sudoku grid contains 36 2-digit unavoidable sets of size 18 for each digit pair (1,2), (1,3)...(8,9).
Depending on the grid, such set may, or may not be split into unavoidable subsets of size: | Code: | 18
14+4
12+6
10+8
10+4+4
8+6+4
6+6+6
6+4+4+4
|
Respectively there are 84 3-digit UA sets of size 36, up to one trivial 9-digit UA of size 81.
Someone may want to calculate the probabilities for each of the combinations.
Regardless of the exact distribution, there is a trend some combinations of UA to exist in a grid more probably than others. This, at least parially, explains the existence of islands in the above graphics.
Finally, there is a difference between the trivial unavoidables for 2 and 3+ digits since latest require more than one clue to be solved.
Distribution of Solution Grids for known 17, 18, 37, 38, and 39-clue puzzles
Here are some pictures representing the distrubution of the grids known to have n-clue puzzles.
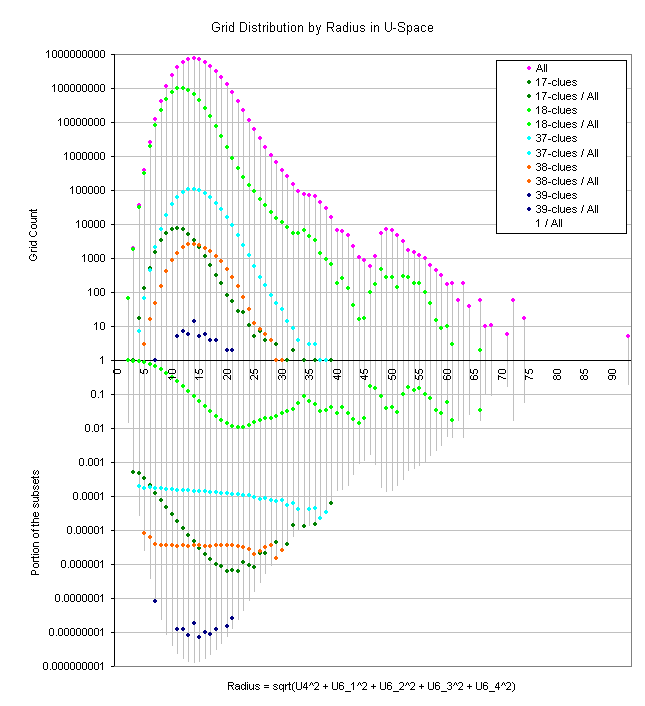
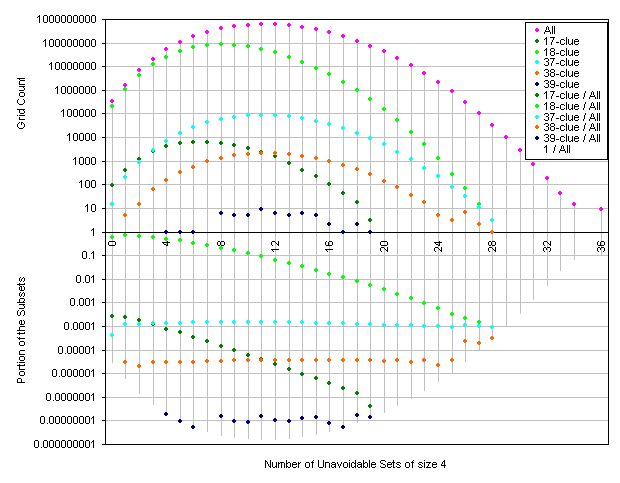
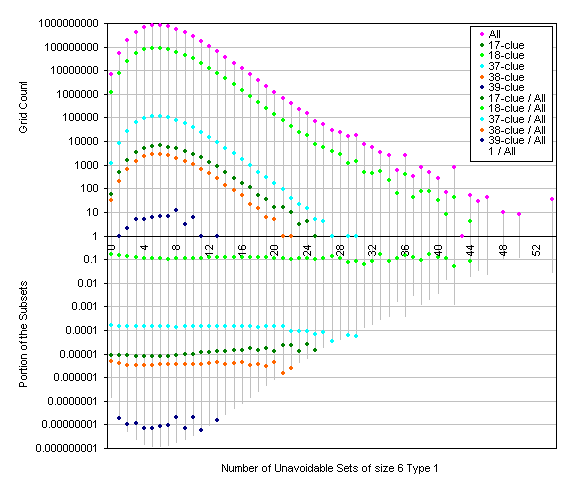
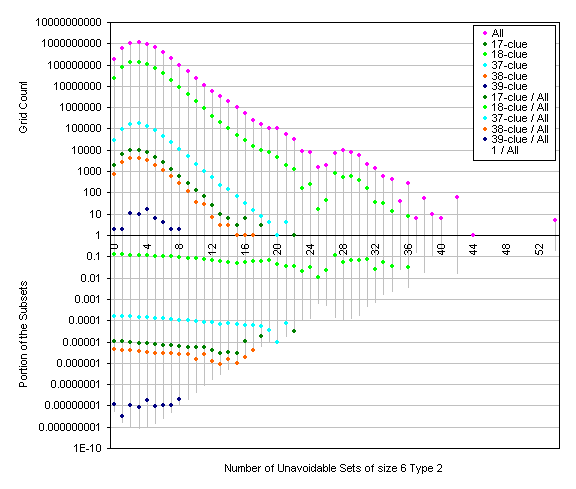
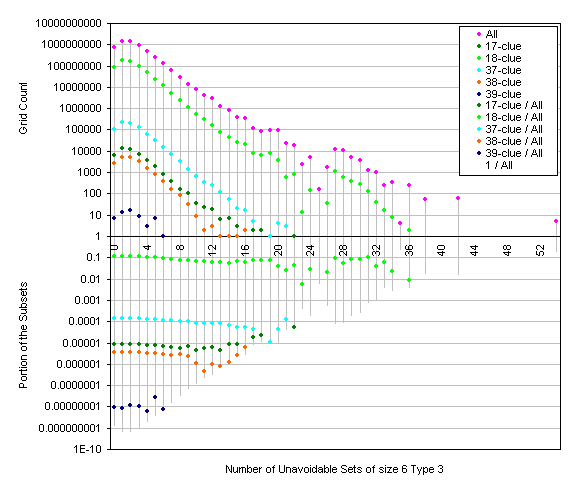
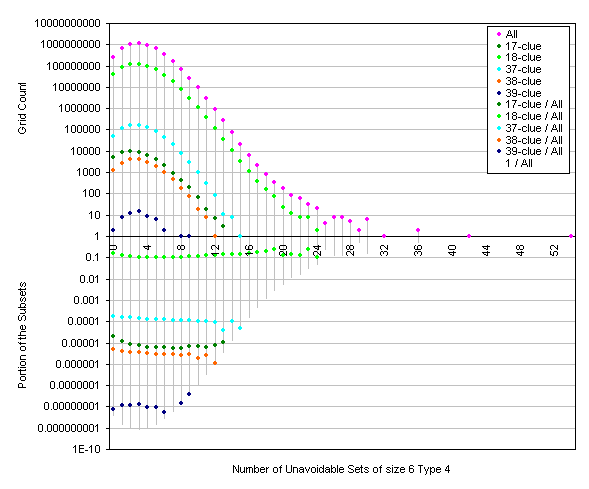
The smoothness of the proportion explains the flattening mentioned in the previous posts.
Grids with least UA
For the processed UA types (2-digit UA of size 4 and 6, and 3-digit UA of size 6) the top three grids are
| Code: |
123456789456789132789213645275941368638527914941638257394175826517862493862394571 #minlex 777870326 3xU6 MCN8(70+11)
123456789456789231789231564234968175867125493915374826348617952592843617671592348 #minlex 1058269476 3xU6 MCN7(65+16)
123456789456789231789231564218593647347628195695174823531962478864317952972845316 #minlex 1057946268 1xU4+2xU6 MCN8(67+14)
123456789456789231798213645239174856574628913681395427367841592815962374942537168 #minlex 1074133462 2xU4+1xU46 MCN8(74+7)
|
where
-minlex is the zero-based index of the grid in the minimal lexical row catalogue
-MCN is the Maximum Clique Number
-in the parenthesis the first number is the cells covered by the UA sets forming one of the cliques.
Cheers,
MD
Last edited by dobrichev on Tue Apr 06, 2010 11:52 pm; edited 1 time in total |
|
| Back to top |
|
 |
| dobrichev
| | Joined: 18 Dec 2009 | | Posts: 28 | | : | |
Items |
|
 Posted: Fri Mar 26, 2010 2:05 pm Post subject: Source Code Posted: Fri Mar 26, 2010 2:05 pm Post subject: Source Code |
 |
|
| The source code in C++ used for grid processing is here. |
|
| Back to top |
|
 |
| dobrichev
| | Joined: 18 Dec 2009 | | Posts: 28 | | : | |
Items |
|
 Posted: Wed Apr 07, 2010 12:46 am Post subject: Update Posted: Wed Apr 07, 2010 12:46 am Post subject: Update |
 |
|
With cooperation of Ano1 the data for a collection of 18-clue puzzles is available. The above pictures are updated and a link to the tabular data for 18's is added. All 4 of the extreme grids published in the previous post have 18-clus puzzles.
The gridsets for 17's and 39's are updated to reflect the recently discovered puzzles (49151 and 65 resp.).
There is one new picture for the proportion between the solution grids of the known extreme-clue puzzles and their less extreme adjacent gridset.
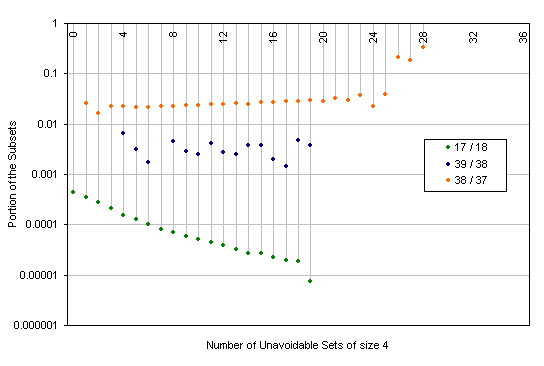
A solution grid known to have 18-clue puzzle is more likely to have 17-clue one if it has less unavoidable sets of size 4. No similar correlation for the high-clue puzzles.
Finally, the second of the extreme grids in the previous post has been scanned for 17's w/o success
| Code: | ....
460799/460800 (3131176643 puzzles gen'd; 0 uniques found); ETTF 0d 00h 00m
Time spent in solver: 9.7% (30195 puzzles / second).
Finished. Total computation time was 12d 09h 00m.
A full search was done (all puzzles were enumerated).
No 17-puzzle exists for this grid (all puzzles were solved).
No pseudo-16-puzzle exists for this grid (all puzzles were solved).
Any puzzles or pseudo-puzzles found were saved to
3_2-17-puzzles.txt respectively 3_2-pseudo-16-puzzles.txt. |
MD. |
|
| Back to top |
|
 |
|
|
You cannot post new topics in this forum
You cannot reply to topics in this forum
You cannot edit your posts in this forum
You cannot delete your posts in this forum
You cannot vote in polls in this forum
|

Powered by phpBB © 2001, 2005 phpBB Group
Igloo Theme Version 1.0 :: Created By: Andrew Charron |










