| View previous topic :: View next topic |
| Author |
Message |
| albertteng
| | Joined: 16 Apr 2009 | | Posts: 4 | | : | |
Items |
|
 Posted: Thu Apr 16, 2009 3:03 am Post subject: A very hard sudoku puzzle please try it |
 |
|
As below it is a very hard sudoku puzzle I created with my program please try it
x x 5 8 x 1 x 2 x
x 8 x x 4 6 9 x x
x x x x x x 1 x x
8 x x x 6 x x 7 x
x x 9 x x x 2 x x
x 5 x x x x x x 1
x x 3 x x x x x x
x x 2 1 3 7 x 6 x
x x x 9 x 5 7 x x
clues: 25
level: very hard
By :Albert.Teng From Taiwan |
|
| Back to top |
|
 |
| Lunatic
 | | Joined: 11 Mar 2007 | | Posts: 166 | | : | | Location: Ghent - Belgium |
Items |
|
| Posted: Fri Apr 17, 2009 10:16 am Post subject: |
|
|
My program, MPQ Sudoku, solved that puzzle, but needed one bifurcation.
This is the Solve Log:
Hidden Single 1 in box at cell E5
Hidden Single 8 in box at cell J3
Hidden Single 6 in box at cell G4
Hidden Single 4 in box at cell G6
Hidden Single 8 in box at cell G5
Hidden Single 2 in row at cell G9
Hidden Single 5 in column at cell C5
Naked Single 5 at cell G7
Hidden Single 5 in box at cell H1
Naked Single 2 at cell J5
Empty Rectangle: Removed candidate 2 from cell D4
Empty Rectangle: Removed candidate 6 from cell C9
Pointing Pair: Row A => Removed candidate 6 from cell(s) A1 A2
Multi Coloring: 1st Conjugate Chain End-Cell=A5 2nd Conjugate Chain End-Cell=H2 => Candidate 9 removed from cell(s) A2
AIC: Weak discontinuity on candidate 2 in cell B1. Chain through cells/candidates B1/1 B3/1 D3/1 D2/1 D2/2 C2/2 and back to cell B1 who looses candidate 2 as solution.
Hidden Single 2 in row at cell B4
Pointing Pair: Row C => Removed candidate 3 from cell(s) C1 C2 C8 C9
AIC: Weak discontinuity on candidate 7 in cell C2. Chain through cells/candidates C2/2 C1/2 F1/2 D2/2 D2/1 D3/1 B3/1 B3/7 and back to cell C2 who looses candidate 7 as solution.
AIC: Weak discontinuity on candidate 1 in cell J1. Chain through cells/candidates J8/1 G8/1 G8/9 F8/9 D9/9 D6/9 D6/2 D2/2 D2/1 D3/1 B3/1 B1/1 and back to cell J1 who looses candidate 1 as solution.
Bifurcation placed candidate 1 at cell D3
Hidden Single 1 in box at cell B1
Naked Single 7 at cell B3
Pointing Pair: Row A => Removed candidate 3 from cell(s) A7 A9
Box Line Reduction: Column 7 => Removed candidate 3 from cell(s) D9 E8 E9 F8
AIC: Weak discontinuity on candidate 7 in cell E4. Chain through cells/candidates E2/7 G2/7 G2/1 G8/1 G8/9 F8/9 D9/9 D6/9 F5/9 F5/7 and back to cell E4 who looses candidate 7 as solution.
Pointing Pair: Row F => Removed candidate 7 from cell(s) F1
AIC: Weak discontinuity on candidate 4 in cell E2. Chain through cells/candidates E2/7 E1/7 G1/7 G1/9 G8/9 F8/9 D9/9 H9/9 H2/9 H2/4 and back to cell E2 who looses candidate 4 as solution.
AIC: Weak discontinuity on candidate 3 in cell E2. Chain through cells/candidates E2/7 E1/7 G1/7 G1/9 G8/9 H9/9 H2/9 H2/4 A2/4 A2/3 and back to cell E2 who looses candidate 3 as solution.
AIC: Weak discontinuity on candidate 8 in cell E8. Chain through cells/candidates E6/8 E6/3 C6/3 C6/9 A5/9 A5/7 A9/7 C9/7 C9/8 C8/8 and back to cell E8 who looses candidate 8 as solution.
AIC: Weak discontinuity on candidate 3 in cell D4. Chain through cells/candidates D4/5 D9/5 B9/5 B9/3 B8/3 B8/5 E8/5 E8/4 D7/4 D7/3 and back to cell D4 who looses candidate 3 as solution.
AIC: Weak discontinuity on candidate 7 in cell G2. Chain through cells/candidates G2/1 G8/1 G8/9 F8/9 D9/9 D6/9 C6/9 C6/3 C4/3 C4/7 A5/7 A9/7 A9/6 A7/6 F7/6 E9/6 E2/6 E2/7 and back to cell G2 who looses candidate 7 as solution.
Hidden Single 7 in box at cell G1
Hidden Single 7 in box at cell E2
Pointing Pair: Column 2 => Removed candidate 9 from cell(s) C2
AIC: Weak discontinuity on candidate 4 in cell C1. Chain through cells/candidates C1/2 C2/2 C2/6 J2/6 J1/6 J1/4 and back to cell C1 who looses candidate 4 as solution.
AIC: Weak discontinuity on candidate 9 in cell D6. Chain through cells/candidates D6/2 D2/2 C2/2 C1/2 C1/9 A1/9 A5/9 A5/7 F5/7 F5/9 and back to cell D6 who looses candidate 9 as solution.
Hidden Single 9 in row at cell D9
Hidden Single 9 in box at cell G8
Hidden Single 9 in box at cell H2
Hidden Single 1 in box at cell J8
Hidden Single 3 in box at cell J9
Hidden Single 3 in box at cell B8
Hidden Single 5 in row at cell D4
Hidden Single 5 in column at cell E8
Naked Single 5 at cell B9
Naked Single 1 at cell G2
X-Wing in Columns: Column1=2 Column2=7 => Removed candidate 4 from cell(s) F1 C2 F4 F7 C9
Hidden Single 4 in box at cell E4
XY-Wing: X=F8 Y1=F3 Y2=E9 => Candidate 6 removed from cell(s) E1 F7
Hidden Single 6 in box at cell E9
Hidden Single 6 in box at cell A7
Hidden Single 8 in row at cell E6
Naked Single 3 at cell E1
Hidden Single 3 in box at cell A2
XY-Wing: X=C2 Y1=D2 Y2=C3 => Candidate 4 removed from cell(s) F3
Hidden Single 4 in box at cell D2
Hidden Single 2 in box at cell F1
Hidden Single 2 in box at cell C2
Hidden Single 2 in box at cell D6
Hidden Single 4 in box at cell F8
Hidden Single 4 in box at cell A9
Hidden Single 4 in box at cell C3
Hidden Single 6 in box at cell C1
Hidden Single 7 in box at cell C9
Hidden Single 7 in box at cell A5
Hidden Single 9 in box at cell C6
Hidden Single 7 in box at cell F4
Hidden Single 8 in box at cell F7
Naked Single 9 at cell A1
Naked Single 3 at cell C4
Naked Single 8 at cell C8
Naked Single 3 at cell D7
Naked Single 6 at cell F3
Naked Single 9 at cell F5
Naked Single 3 at cell F6
Naked Single 4 at cell H7
Naked Single 8 at cell H9
Naked Single 4 at cell J1
Naked Single 6 at cell J2
Sudoku solved
_________________
Marc
~~~<><~~~<><~~~<><~~~<><~~~
Last edited by Lunatic on Sat Apr 18, 2009 6:21 am; edited 1 time in total |
|
| Back to top |
|
|
| hobiwan
| | Joined: 11 Feb 2008 | | Posts: 83 | | : | |
Items |
|
| Posted: Fri Apr 17, 2009 2:45 pm Post subject: |
|
|
Nice Puzzle! HoDoKu needed 12 chains, 1 ALS, 2 fishes and some smaller moves.
Keep on with your good work! |
|
| Back to top |
|
|
| Lunatic
| | Joined: 11 Mar 2007 | | Posts: 166 | | : | | Location: Ghent - Belgium |
Items |
|
| Posted: Sat Apr 18, 2009 6:18 am Post subject: |
|
|
| hobiwan wrote: | Nice Puzzle! HoDoKu needed 12 chains, 1 ALS, 2 fishes and some smaller moves.
|
Very nice program, hobiwan.
Where my program needed the Bifurcation, that's where your program spotted the ALS.
_________________
Marc
~~~<><~~~<><~~~<><~~~<><~~~ |
|
| Back to top |
|
|
| hobiwan
| | Joined: 11 Feb 2008 | | Posts: 83 | | : | |
Items |
|
| Posted: Sat Apr 18, 2009 5:06 pm Post subject: |
|
|
| Lunatic wrote: | | Very nice program, hobiwan. |
Thanks! |
|
| Back to top |
|
|
| albertteng
| | Joined: 16 Apr 2009 | | Posts: 4 | | : | |
Items |
|
| Posted: Tue Apr 21, 2009 2:58 am Post subject: |
|
|
hobiwan wrote
many thanks !!
Your program is very powerful
Albert.Teng |
|
| Back to top |
|
|
| lkSudoku
| | Joined: 16 May 2009 | | Posts: 60 | | : | |
Items |
|
| Posted: Thu May 21, 2009 1:26 pm Post subject: |
|
|
| This puzzle seem to be a hard puzzle |
|
| Back to top |
|
|
| lkSudoku
| | Joined: 16 May 2009 | | Posts: 60 | | : | |
Items |
|
| Posted: Thu May 21, 2009 3:29 pm Post subject: |
|
|
While at trying very hard sudoku puzzles, my sudoku puzzle generator has a puzzles level named "requires guess", I add here a set of 4 generated puzzles in that level, could you tell if these 4 puzzles realy require guessing? or perhaps they do have a logical solution?
| Code: |
. 3 . |. 2 5 |7 . .
1 . . |. 3 4 |. . .
. . . |. . . |. 6 .
------+------+-----
5 . . |8 . . |. . .
6 . . |. . 3 |. . 7
. . 1 |. . . |. 2 6
------+------+-----
. . 2 |. . . |. . 9
. 4 . |7 . . |. . .
. . . |2 . . |6 8 .
|
| Code: |
. . 8 |3 1 . |6 . .
. . . |. . 4 |. . .
. . . |. 9 . |. . 3
------+------+-----
. . . |5 . 9 |. . .
8 . . |1 . . |. 3 .
6 . 2 |. . . |8 . 9
------+------+-----
2 5 . |6 . . |. . .
. . 9 |. 2 . |. . 7
. . . |. . . |1 . .
|
| Code: |
. . . |6 7 . |. . 9
1 6 . |. . . |. . .
. . . |. . . |. 5 .
------+------+-----
. . . |. . 8 |4 . .
. . 4 |. . . |8 1 .
. 7 . |. . 9 |. . .
------+------+-----
. 3 . |9 5 . |. . .
8 . . |. . . |. . .
4 . . |. 2 . |1 7 3
|
| Code: |
. . . |3 . . |9 . 8
. . . |. . 8 |5 . .
. . . |. 9 . |. . 1
------+------+-----
9 5 2 |. . 4 |6 . .
. . . |. . . |. . 5
8 . . |. . . |4 1 .
------+------+-----
. . 6 |7 . 9 |3 . .
. . 4 |. . . |. 6 .
5 . 8 |. 6 . |. . 9
|
|
|
| Back to top |
|
|
| hobiwan
| | Joined: 11 Feb 2008 | | Posts: 83 | | : | |
Items |
|
| Posted: Thu May 21, 2009 4:30 pm Post subject: |
|
|
| lkSudoku wrote: | | could you tell if these 4 puzzles realy require guessing? or perhaps they do have a logical solution? |
If your logic gets complex enough then very probably every puzzle can be solved without guessing.
The HoDoKu ratings for your puzzles:
#1: Unfair 2242 (3 XY-Chains) SE 7.2
#2: Hard 532 (1 Skyscraper only) SE 6.6
#3: Unfair 1626 (2 XY-Chains) SE 7.2
#4: Unfair 2180 (1 AIC) SE 7.2
The puzzles are hard, but not very hard (XY-Chains are among the simpler types of chains).
[edit: added SE ratings]
Last edited by hobiwan on Thu May 21, 2009 5:50 pm; edited 1 time in total |
|
| Back to top |
|
|
| lkSudoku
| | Joined: 16 May 2009 | | Posts: 60 | | : | |
Items |
|
| Posted: Thu May 21, 2009 4:42 pm Post subject: |
|
|
| The HoDoKu solver seems quite strong indeed |
|
| Back to top |
|
|
| hobiwan
| | Joined: 11 Feb 2008 | | Posts: 83 | | : | |
Items |
|
| Posted: Thu May 21, 2009 5:49 pm Post subject: |
|
|
| lkSudoku wrote: | | The HoDoKu solver seems quite strong indeed |
Not really. It has a lot of different techniques implemented, but it stops at around SE 9.3 (SE ratings of hardest puzzles go up to 14). I edited my post above to show the SE ratings of your puzzles. |
|
| Back to top |
|
|
| lkSudoku
| | Joined: 16 May 2009 | | Posts: 60 | | : | |
Items |
|
| Posted: Fri May 22, 2009 2:32 pm Post subject: |
|
|
That makes me wonder, is there an example for a sudoku board which realy does requires guessing and has no logical solution by all known logical solutions so far?
A board that cannot be solved by HoDoKu, SE, or any other solver?
If there is such a board, can anyone post it here? |
|
| Back to top |
|
|
| JasonLion
| | Joined: 16 Nov 2008 | | Posts: 62 | | : | | Location: Silver Spring, MD |
Items |
|
| Posted: Fri May 22, 2009 11:07 pm Post subject: |
|
|
| There are many solvers that can solve every puzzle. It really has to do with what you call "logical". All of the solvers that can solve every puzzle use some method that I call trial and error, and which would be impractical for a person to use, but most of these methods are also logical. |
|
| Back to top |
|
|
| NewUrbanBlues
| | Joined: 22 Oct 2006 | | Posts: 36 | | : | |
Items |
|
| Posted: Sun May 24, 2009 8:22 am Post subject: |
|
|
| lkSudoku wrote: | While at trying very hard sudoku puzzles, my sudoku puzzle generator has a puzzles level named "requires guess", I add here a set of 4 generated puzzles in that level, could you tell if these 4 puzzles realy require guessing? or perhaps they do have a logical solution?
[/code] |
Hello IkSudoku
Here are the results with Isanaki Sudoku v 2.5
Code1: Guess required
01 Single in a Box 46
02 Single in a Row 2
03 Single in a Column 5
04 Naked Single in a Row, a Box or a Column 3
05 Hidden Single in a Column 1
06 Locked Candidates Type 1 in a Row 3
07 Locked Candidates Type 1 in a Column 4
08 Locked Candidates Type 2 in a Row 2
09 Locked Candidates Type 2 in a Column 1
10 Naked Pair in a Box 1
11 Naked Pair in a Row 1
12 Naked Triple in a Box 1
13 Brute Force Guess 1
Code2: surprisingly, no guess required
01 Single in a Box 48
02 Single in a Row 2
03 Naked Single in a Row, a Box or a Column 6
04 Hidden Single in a Box 1
05 Hidden Single in a Row 1
06 Locked Candidates Type 1 in a Column 1
07 Single Colours Type I 1
Code 3: guess required
01 Single in a Box 49
02 Single in a Row 2
03 Single in a Column 2
04 Naked Single in a Row, a Box or a Column 2
05 Hidden Single in a Box 2
06 Hidden Single in a Column 1
07 Locked Candidates Type 1 in a Row 2
08 Locked Candidates Type 1 in a Column 4
09 Naked Pair in a Box 2
10 Naked Pair in a Row 1
11 Naked Pair in a Column 2
12 Unique Rectangle Type I 1
13 Brute Force Guess 1
Code 4: few techniques but guess required
01 Single in a Box 49
02 Single in a Column 4
03 Locked Candidates Type 2 in a Row 2
04 Hidden Pair in a Row 1
05 Single Colours Type I 1
06 Brute Force Guess 2
Thierry |
|
| Back to top |
|
|
| strmckr
 | | Joined: 24 Apr 2009 | | Posts: 52 | | : | |
Items |
|
| Posted: Mon May 25, 2009 8:09 am Post subject: |
|
|
Fata Morgana
| Code: | *-----------*
|...|...|..3|
|..1|..5|6..|
|.9.|.4.|.7.|
|---+---+---|
|...|..9|.5.|
|7..|...|..8|
|.5.|4.2|...|
|---+---+---|
|.8.|.2.|.9.|
|..3|5..|1..|
|6..|...|...|
*-----------* |
| Code: | *-----------------------------------------------------------------------------*
| 2458 2467 245678 | 126789 16789 1678 | 24589 1248 3 |
| 2348 2347 1 | 23789 3789 5 | 6 248 249 |
| 2358 9 2568 | 12368 4 1368 | 258 7 125 |
|-------------------------+-------------------------+-------------------------|
| 12348 12346 2468 | 13678 13678 9 | 2347 5 12467 |
| 7 12346 2469 | 136 1356 136 | 2349 12346 8 |
| 1389 5 689 | 4 13678 2 | 379 136 1679 |
|-------------------------+-------------------------+-------------------------|
| 145 8 457 | 1367 2 13467 | 3457 9 4567 |
| 249 247 3 | 5 6789 4678 | 1 2468 2467 |
| 6 1247 24579 | 13789 13789 13478 | 234578 2348 2457 |
*-----------------------------------------------------------------------------* |
| Quote: | A board that cannot be solved by HoDoKu, SE, or any other solver?
If there is such a board, can anyone post it here? |
this is the closest board there is: but as suggested above depends on what you deem a logic construct.
this puzzle has stopped many of the unavliable to the public logic solvers:
and all the ones that are.
Alan Barker's solver uses logic and produced the first solution to it using coverset algorithums.
every other solver to date cannot solve it with out brute force.
there is alot of methods that are logic based many of them become
unpractical or extremly combersum for any human to properly applicate the technique.
the ones i consder brute force use backtracking to find a solution.
what is coded into the solver is where the limit of that solver lies and that is usually where brute force takes over.
the logic that solves this is not brute force either.
its a precies application of sets covering a specific mathmatical arangment so that all arangments yield the same end results.
very complex and solid logic.
this is a graphical form of
14 Sets = {136R3 136R7 136C2 136C8 5N46}
27 Links = {1r5 3r456 6r456 136c4 136c6 4n2 6n8 1b37 3b14569 6b14569}
4 AURs = (13)r35c46 + (16)r35c46 + (13)r57c46 + (16)r57c46
32 Eliminations
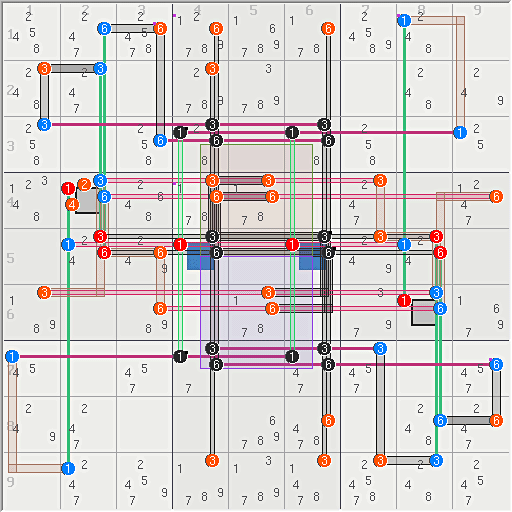
yes every valid grid can be solved logically with out t&e
its simply a matter of how complex the logic is that produces the solution.
and then another if the solver in question contains that method or not. |
|
| Back to top |
|
|
|
FAQ
Search
Memberlist
Usergroups
Register
Profile
Log in
Log in to check your private messages
