
|
| View previous topic :: View next topic |
| Author |
Message |
| Ruud
Site Admin
 | | Joined: 17 Sep 2005 | | Posts: 708 | | : | | Location: Netherlands |
Items |
|
 Posted: Fri Mar 10, 2006 9:29 pm Post subject: Hunting finned X-Wing and other fishy stuff Posted: Fri Mar 10, 2006 9:29 pm Post subject: Hunting finned X-Wing and other fishy stuff |
 |
|
As requested by Ron, here is my approach to finding finned X-Wings.
What the heck is a finned X-Wing?
If you do not know what an X-Wing is, read about it here: http://www.simes.clara.co.uk/programs/sudokutechnique6.htm
A finned X-Wing is almost an X-Wing. The only difference is that one of the 4 cells has some extra candidates that share a box and a row or column (depending on whether the almost X-Wing lies in the rows or in the columns.
This is the picture:
| Code: | . . .|. . .|. . .
. . .|. . .|. . .
. . X|. x .|. . .
-----+-----+-----
. . *|. . .|. . .
. . *|. . .|. . .
F F x|. X .|. . .
-----+-----+-----
. . .|. . .|. . .
. . .|. . .|. . .
. . .|. . .|. . . |
The extra candidates (marked with F) is what people call the 'fin'. Either of these 2 candidates can be available, or both.
There are 3 possible solutions to this pattern:
Solution 1:
| Code: | . . .|. . .|. . .
. . .|. . .|. . .
. . .|. x .|. . .
-----+-----+-----
. . *|. . .|. . .
. . *|. . .|. . .
. . x|. . .|. . .
-----+-----+-----
. . .|. . .|. . .
. . .|. . .|. . .
. . .|. . .|. . . |
Solution 2:
| Code: | . . .|. . .|. . .
. . .|. . .|. . .
. . X|. . .|. . .
-----+-----+-----
. . *|. . .|. . .
. . *|. . .|. . .
. . .|. X .|. . .
-----+-----+-----
. . .|. . .|. . .
. . .|. . .|. . .
. . .|. . .|. . . |
Solution 3:
| Code: | . . .|. . .|. . .
. . .|. . .|. . .
. . .|. x .|. . .
-----+-----+-----
. . *|. . .|. . .
. . *|. . .|. . .
F F .|. . .|. . .
-----+-----+-----
. . .|. . .|. . .
. . .|. . .|. . .
. . .|. . .|. . . |
It is clear that in each of these 3 solutions, the 2 starred candidates are eliminated.
In fact, the candidate in the finned corner is optional. Without it, only solutions 2 and 3 can occur. In both cases the starred candidates are eliminated.
How common is this finned X-Wing?
I have a large collection of Sudokus that required a template exclusion. About 1 in 3 can now be solved with a finned X-Wing, sometimes in combination with coloring. Many Sudokus that could only be solved with multi-coloring can now be solved with a finned X-Wing.
What is more important: It is a very recognizable pattern for human players. Just as easy to spot as the normal X-Wing.
Finned what-else is there?
Yes, there is a finned swordfish. Anything bigger? Not that I know of, but it would not surprise me. Larger patterns are no longer easily recognized by human players, same as with the unfinned counterparts.
How can we find them?
This is the part that I have some trouble with. When both defining rows are in the same chute, the 3rd box in that chute would have locked candidates or a single and no eliminations would be left for the finned X-Wing.
The following pattern would be a valid finned X-Wing, I think:
| Code: | . . .|. . .|. . .
. . .|. . .|. . .
- X X|- - -|- - -
-----+-----+-----
. . *|. . .|. . .
. . *|. . .|. . .
F X X|- - -|- - -
-----+-----+-----
. . .|. . .|. . .
. . .|. . .|. . .
. . .|. . .|. . . |
Some Pseudo Code
Because the finned structure is irregular, it is not possible to reuse the compact algorithm that is used for finding X-Wings.
For each digit missing 3 or more placements
- For each row A with exactly 2 candidates for that digit
- - For each row B in the other 2 floors
- - - If row B contains one candidate in the same row as one of the candidates in row A, and all other candidates in the same tower as the other candidate in row A
- - - - candidates in the intersection of the finned column and the box containing the fin, except those on row B can be eliminated.
- (swap row with column and tower with floor and do it again)
Questions
What can be improved here?
How do we deal with finned swordfish?
Is is possible to write a generic search algorithm for both?
Can we find (and catch) finned jellyfish?
Ruud.
_________________
Meet me at sudocue.net |
|
| Back to top |
|
 |
| gsf
| | Joined: 18 Aug 2005 | | Posts: 411 | | : | | Location: NJ USA |
Items |
|
 Posted: Fri Mar 10, 2006 10:28 pm Post subject: Re: Hunting finned X-Wing and other fishy stuff Posted: Fri Mar 10, 2006 10:28 pm Post subject: Re: Hunting finned X-Wing and other fishy stuff |
 |
|
nice post
it would be nicer if a few real puzzle examples were posted or referenced along with the illustrative pseudo examples |
|
| Back to top |
|
 |
| foxglove
| | Joined: 04 Feb 2006 | | Posts: 42 | | : | | Location: Portugal |
Items |
|
 Posted: Fri Mar 10, 2006 10:53 pm Post subject: one question Posted: Fri Mar 10, 2006 10:53 pm Post subject: one question |
 |
|
| what's the difference between a finned X-Wing and a Turbot? |
|
| Back to top |
|
 |
| Ruud
Site Admin
 | | Joined: 17 Sep 2005 | | Posts: 708 | | : | | Location: Netherlands |
Items |
|
 Posted: Fri Mar 10, 2006 11:16 pm Post subject: Posted: Fri Mar 10, 2006 11:16 pm Post subject: |
 |
|
I almost forgot! 
here are a few examples to demonstrate the finned X-Wing:
This sudoku could not be solved without a template check or stronger techniques. It can now be solved with a nice sequence of a naked triple, 2 naked singles, a finned X-Wing and another naked triple that finally breaks it. This sudoku would have been classified as extremely tough, but with finned X-Wing, it is just a hard one.
| Code: | . . .|. . 2|. 4 .
. . 7|. 4 .|. 3 .
. . 6|. . .|1 . 9
-----+-----+-----
. 8 .|. . 9|. . .
3 . 9|. 6 .|8 . 5
. . .|7 . .|. 1 .
-----+-----+-----
6 . 5|. . .|4 . .
. 1 .|. 8 .|2 . .
. 7 .|3 . .|. . . |
Another example. Solves with a hidden pair, a finned X-Wing and a naked triple:
| Code: | . 8 .|5 6 .|. 1 .
. 7 3|. . .|. . .
4 . .|. . .|. . 2
-----+-----+-----
. . .|2 . .|3 . .
. . 8|. 7 .|9 . .
. . 2|. . 3|. . .
-----+-----+-----
1 . .|. . .|. . 9
. . .|. . .|1 7 .
. 6 .|. 3 5|. 8 . |
The next example demonstrates how finned X-Wing can play a role in a multiple technique solving strategy. This sudoku solves with finned X-Wings, a swordfish, several line-box reductions and an XY-Wing.
| Code: | . . .|7 . .|. 5 .
. 2 9|. 5 .|. . .
. 5 7|. . .|8 4 .
-----+-----+-----
5 . .|. . 4|. . .
. . 6|. 9 .|3 . .
. . .|5 . .|. . 8
-----+-----+-----
. 8 4|. . .|7 1 .
. . .|. 4 .|5 6 .
. 9 .|. . 6|. . . |
And finally, the only thing heavier than line-box reductions in this sudoku are 2 finned X-Wings in a row:
| Code: | . 7 .|2 . .|. . .
. . 3|5 9 .|2 . .
. . 8|. . 1|. 4 .
-----+-----+-----
4 . .|. . .|. 3 .
2 . .|. 3 .|. . 7
. 6 .|. . .|. . 9
-----+-----+-----
. 9 .|3 . .|8 . .
. . 6|. 5 4|1 . .
. . .|. . 9|. 6 . |
This is the point where the first of these finned X-Wings appears:
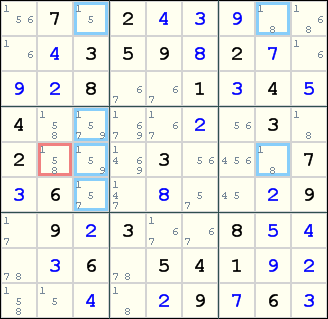
And this is the second finned X-Wing:
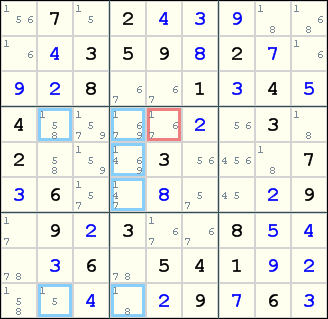
Ruud |
|
| Back to top |
|
 |
| rkral
| | Joined: 21 Oct 2005 | | Posts: 233 | | : | |
Items |
|
 Posted: Sat Mar 11, 2006 12:12 pm Post subject: Posted: Sat Mar 11, 2006 12:12 pm Post subject: |
 |
|
| Ruud wrote: | | here are a few examples to demonstrate the finned X-Wing: |
Great examples, Ruud. I found a finned X-wing in your first three examples, but mine didn't always lead to a solution, and didn't always have the same path to solution as you indicated. But I'm not really concerned about the 'solution' part, as I'm mainly interested in identifying them.
I am IDing the finned fishies manually ... and spotting them in your examples was a challenge. I found finned x-wings as follows: in ex. 1, at r29c67 in 5s; in ex. 2, at r26c47 in 8s; and in ex. 3, one at r25c16 in 1s and another at r39c15 in 3s. (When posting examples, perhaps you could post the answer -- briefly and somewhat displaced from the puzzle itself -- for those who might just give up before finding anything.)
Part of my purpose in participating in this forum is to try to decide whether to first implement (in my solver) finned fishies or grouped coloring. So, if you don't mind my going "off-topic", I'd like to play devil's advocate a bit and illustrate how exclusions made with finned x-wing, etc. can also be made with grouped coloring.
[edit: In the above paragraph, I mean on a pattern-by-pattern basis (finned x-wing, swordfish, etc.), not on a puzzle-by-puzzle basis. Let me know if that's OK.]
I don't think grouped coloring can replace finned N-fish entirely, but it might be interesting to discover the cases grouped coloring cannot do.
Ron |
|
| Back to top |
|
 |
| tarek
| | Joined: 31 Dec 2005 | | Posts: 153 | | : | | Location: London, UK |
Items |
|
 Posted: Sat Mar 11, 2006 2:02 pm Post subject: Posted: Sat Mar 11, 2006 2:02 pm Post subject: |
 |
|
Hi there Ruud,
I generated this puzzle which is the perfect answer to finned x-wing galore..........
You can add it to you list of examples if you want.......
example4:
| Code: | . . . | 2 3 . | . 5 .
. . . | 9 . 5 | 4 . .
. . . | . 8 . | . 9 3
-------+-------+------
. 3 . | . . . | . 4 9
1 . . | . . 3 | . . 7
5 2 . | . 1 . | . . 8
-------+-------+------
9 6 . | 3 . . | . . .
. . 4 | . . . | . . .
. . . | 7 9 2 | . . . |
And here is a twin without the XY wing
example5:
| Code: | . . . | 2 3 . | . 5 .
. . . | 9 . 5 | 4 . .
. . . | . 8 . | . . 3
-------+-------+------
8 3 . | . 2 . | . 4 9
1 . 9 | 8 . 3 | 5 . 7
5 . . | . 1 . | . 6 8
-------+-------+------
9 6 . | 3 4 . | . . .
. . 4 | . . . | . . .
. . . | 7 9 2 | . . . |
I note that you do not describe the Sashimi variation of the finned x-wing or what is prbably better referred to as the Almost finned x-wing [just modifying your example].....
| Code: | . . .|. . .|. . .
. . .|. . .|. . .
. . X|. x .|. . .
-----+-----+-----
. . *|. . .|. . .
. . *|. . .|. . .
F F .|. X .|. . .
-----+-----+-----
. . .|. . .|. . .
. . .|. . .|. . .
. . .|. . .|. . . |
would achieve the same result, note that the missing vertix at r6c3 did not affect the outcome (As if it was still there, hence the word Almost)...
Tarek
Last edited by tarek on Sat Mar 11, 2006 5:49 pm; edited 1 time in total |
|
| Back to top |
|
 |
| rkral
| | Joined: 21 Oct 2005 | | Posts: 233 | | : | |
Items |
|
 Posted: Sat Mar 11, 2006 4:03 pm Post subject: Posted: Sat Mar 11, 2006 4:03 pm Post subject: |
 |
|
| tarek wrote: | I generated this puzzle which is the perfect answer to finned x-wing galore
..........
And here is a twin without the XY wing
|
Not knowing both the digit and the candidate grid at the time of the pattern often obscures the communication. Therefore, I suggest posting the candidate grid at the time of the pattern -- with optional identification of the pattern -- and the starting grid in condensed one-line format. Using your first puzzle as an example, it might look something like: | Code: |
Finned x-wing in 1s at r29c28:
...23..5....9.54......8..93.3.....491....3..752..1...896.3.......4.........792...
4678 9 168 | 2 3 146 | 78 5 16
236 *18 236 | 9 7 5 | 4 *18 26
2467 -157 1256 | 16 8 146 | 27 9 3
-----------------+----------------+---------------
68 3 68 | 5 2 7 | 1 4 9
1 4 9 | 8 6 3 | 5 2 7
5 2 7 | 4 1 9 | 36 36 8
-----------------+----------------+---------------
9 6 128 | 3 4 18 | 28 7 5
2378 +178 4 | 16 5 168 | 9 -138 12
38 *158 #1358 | 7 9 2 | 36 *1368 4 |
For a little challenge, the digit and the location would be omitted, but the candidate grid should always be posted IMO. Ironically, this is most useful for the simpler puzzles ... since these are the puzzles affording multiple ways to proceed.
The notation used within the candidate grids above is the notation currently used by Myth Jellies, the originator of this technique AFAIK. The asterisks (*) identify the almost x-wing, the hashmarks (#) are the candidates preventing the almost x-wing from being an actual x-wing, and the minuses (-) are the candidates that would be eliminated were it an actual x-wing. Of the latter, those minused candidates that see ALL the hashmarked candidates are re-marked with a plus (+) ... and may be eliminated.
Ron
P.S. Off-topic: This HTML page acts like a fixed width page, which inhibits line-wrap. Does anyone know whether that's common to all pages on setbb.com ... or just due to our content on this page? Duh! I can go look at other pages to find out for myself.  |
|
| Back to top |
|
 |
| Ruud
Site Admin
 | | Joined: 17 Sep 2005 | | Posts: 708 | | : | | Location: Netherlands |
Items |
|
 Posted: Sat Mar 11, 2006 5:21 pm Post subject: Posted: Sat Mar 11, 2006 5:21 pm Post subject: |
 |
|
Thank you for pointing out the finned X-Wing.
My solver spotted this XY-Wing at the exact same candidate position:
| Code: | *=root, #=pincers, -=victims, {XYZ}={281}
.---------------.---------------.---------------.
| 4678 9 168 | 2 3 146 | 78 5 16 |
| 236 18 236 | 9 7 5 | 4 18 26 |
| 2467 157 1256| 16 8 146 | 27 9 3 |
:---------------+---------------+---------------:
| 68 3 68 | 5 2 7 | 1 4 9 |
| 1 4 9 | 8 6 3 | 5 2 7 |
| 5 2 7 | 4 1 9 | 36 36 8 |
:---------------+---------------+---------------:
| 9 6 128 | 3 4 #18 |*28 7 5 |
| 2378 178 4 |-16 5 -168 | 9 138 #12 |
| 38 158 1358| 7 9 2 | 36 1368 4 |
'---------------'---------------'---------------' |
This spoiled the finned X-Wing.
Here are the finned X-Wings in my first 3 examples:
| Code: | Finned X-Wing for digit 5
.------------------.------------------.------------------.
| 189 359 38 | 15689 159 2 | 7 4 68 |
| 1289 -259 7 |-15689 4 *156 |*56 3 268 |
| 248 245 6 | 58 7 3 | 1 25 9 |
:------------------+------------------+------------------:
| 7 8 1 | 245 25 9 | 3 26 246 |
| 3 24 9 | 124 6 14 | 8 7 5 |
| 5 6 24 | 7 3 8 | 9 1 24 |
:------------------+------------------+------------------:
| 6 239 5 | 129 129 17 | 4 8 37 |
| 49 1 34 | 4569 8 #4567 | 2 569 37 |
| 2489 7 248 | 3 +259 *456 |*56 -569 1 |
'------------------'------------------'------------------' |
The 2nd puzzle:
| Code: | Finned X-Wing for digit 8
.------------------.------------------.------------------.
| 2 8 9 | 5 6 47 | 47 1 3 |
| 56 7 3 |*489 12 12 |*4568 4569 +568 |
| 4 15 16 | 3 89 789 |#5678 569 2 |
:------------------+------------------+------------------:
| 567 1459 16 | 2 14589 14689| 3 456 15678|
| 3 145 8 | 46 7 146 | 9 2 156 |
| 567 1459 2 |*4689 -14589 3 |*4568 456 -15678|
:------------------+------------------+------------------:
| 1 2 45 | 7 48 468 | 56 3 9 |
| 8 3 45 | 469 249 2469 | 1 7 56 |
| 9 6 7 | 1 3 5 | 2 8 4 |
'------------------'------------------'------------------' |
The 3rd puzzle:
| Code: | Finned X-Wing for digit 1
.---------------.---------------.---------------.
| 4 6 138 | 7 1238-123 | 9 5 12 |
|*18 2 9 | 4 5 *18 | 6 3 7 |
|-13 5 7 | 6 123 9 | 8 4 12 |
:---------------+---------------+---------------:
| 5 37 238 | 23 2378 4 | 1 9 6 |
|*1278 4 6 |#128 9 *1278| 3 27 5 |
| 9 137 123 | 5 6 +1237| 4 27 8 |
:---------------+---------------+---------------:
| 6 8 4 | 239 23 5 | 7 1 39 |
|-1237 137 123 | 1389 4 1378| 5 6 39 |
|-137 9 5 | 13 137 6 | 2 8 4 |
'---------------'---------------'---------------' |
| Code: | Finned X-Wing for digit 3
.---------------.---------------.---------------.
| 4 6 138 | 7 -1238 123 | 9 5 12 |
| 18 2 9 | 4 5 18 | 6 3 7 |
|*13 5 7 | 6 *123 9 | 8 4 12 |
:---------------+---------------+---------------:
| 5 37 238 | 23 -2378 4 | 1 9 6 |
| 278 4 6 | 128 9 1278| 3 27 5 |
| 9 137 123 | 5 6 237 | 4 27 8 |
:---------------+---------------+---------------:
| 6 8 4 | 239 +23 5 | 7 1 39 |
|-1237 137 123 | 1389 4 1378| 5 6 39 |
|*137 9 5 |#13 *137 6 | 2 8 4 |
'---------------'---------------'---------------' |
Ruud. |
|
| Back to top |
|
 |
| tarek
| | Joined: 31 Dec 2005 | | Posts: 153 | | : | | Location: London, UK |
Items |
|
 Posted: Sat Mar 11, 2006 6:06 pm Post subject: Posted: Sat Mar 11, 2006 6:06 pm Post subject: |
 |
|
| rkral wrote: |
Not knowing both the digit and the candidate grid at the time of the pattern often obscures the communication. Therefore, I suggest posting the candidate grid at the time of the pattern -- with optional identification of the pattern -- and the starting grid in condensed one-line format. |
Demanding aren't we.... fair enough
As Example 4 contains an XY wing........it is possible to apply it prior to the finned x-wings --- foiling many of them, however if applied after, then there would be many.
However example 5 has no XY wing as I mentioned, Enjoy
| Code: | 000230050000905400000080003830020049109803507500010068960340000004000000000792000
*--------------------------------------------------------*
| 467 9 178 | 2 3 146 | 78 5 16 |
|*26 -128 3 | 9 7 5 | 4 18 *126 |
|#2467 1257 1257 | 16 8 146 | 27 9 3 |
|------------------+------------------+------------------|
| 8 3 6 | 5 2 7 | 1 4 9 |
| 1 4 9 | 8 6 3 | 5 2 7 |
| 5 27 27 | 4 1 9 | 3 6 8 |
|------------------+------------------+------------------|
| 9 6 128 | 3 4 18 | 28 7 5 |
|*27 1278 4 | 16 5 168 | 9 3 *12 |
| 3 158 158 | 7 9 2 | 6 18 4 |
*--------------------------------------------------------*
Eliminating 2 From r2c2 (Finned XWing in Columns 19)
r2c9 Must only have 26 as valid Candidates (18 is a Naked Double in Row 2)
*--------------------------------------------------------*
| 467 9 178 |*2 3 -146 | 78 5 *16 |
| 26 18 3 | 9 7 5 | 4 18 26 |
| 2467 1257 1257 |#16 8 146 | 27 9 3 |
|------------------+------------------+------------------|
| 8 3 6 | 5 2 7 | 1 4 9 |
| 1 4 9 | 8 6 3 | 5 2 7 |
| 5 27 27 | 4 1 9 | 3 6 8 |
|------------------+------------------+------------------|
| 9 6 128 | 3 4 18 | 28 7 5 |
| 27 1278 4 |*16 5 168 | 9 3 *12 |
| 3 158 158 | 7 9 2 | 6 18 4 |
*--------------------------------------------------------*
Eliminating 1 From r1c6 (Finned XWing in Columns 49)----Sashimi variation (Almost finned x-wing)
Eliminating 1 From r3c2 (Box 2 & Row 3 Box-Line interaction)
Eliminating 1 From r3c3 (Box 2 & Row 3 Box-Line interaction)
r1c3 Must only have 18 as valid Candidates (18 is a Hidden Double in Box 1)
r3c1 Must only have 46 as valid Candidates (146 is a Hidden Triple in Row 3)
Eliminating 2 From r8c2 (XWing in Columns 19)
*-----------------------------------------------*
| 467 9 18 | 2 3 46 | 78 5 16 |
| 26 *18 3 | 9 7 5 | 4 *18 26 |
| 46 257 257 | 16 8 146 | 27 9 3 |
|---------------+---------------+---------------|
| 8 3 6 | 5 2 7 | 1 4 9 |
| 1 4 9 | 8 6 3 | 5 2 7 |
| 5 27 27 | 4 1 9 | 3 6 8 |
|---------------+---------------+---------------|
| 9 6 128 | 3 4 18 | 28 7 5 |
| 27 #178 4 | 16 5 168 | 9 3 12 |
| 3 *158 -158 | 7 9 2 | 6 *18 4 |
*-----------------------------------------------*
Eliminating 1 From r9c3 (Finned XWing in Columns 28)
Eliminating 1 From r8c2 ( XWing in Rows 29)
*-----------------------------------------------*
| 467 9 18 | 2 3 46 | 78 5 16 |
| 26 *18 3 | 9 7 5 | 4 *18 26 |
| 46 257 257 | 16 8 146 | 27 9 3 |
|---------------+---------------+---------------|
| 8 3 6 | 5 2 7 | 1 4 9 |
| 1 4 9 | 8 6 3 | 5 2 7 |
| 5 27 27 | 4 1 9 | 3 6 8 |
|---------------+---------------+---------------|
| 9 6 128 | 3 4 18 | 28 7 5 |
| 27 #78 4 | 16 5 168 | 9 3 12 |
| 3 *158 -58 | 7 9 2 | 6 *18 4 |
*-----------------------------------------------*
Eliminating 8 From r9c3 (Finned XWing in Columns 28) -----Which could have been combined with last Finned x-wing |
|
|
| Back to top |
|
 |
| Ruud
Site Admin
 | | Joined: 17 Sep 2005 | | Posts: 708 | | : | | Location: Netherlands |
Items |
|
 Posted: Sat Mar 11, 2006 6:45 pm Post subject: Posted: Sat Mar 11, 2006 6:45 pm Post subject: |
 |
|
Hi Tarek,
I am still foiled by an XY-Wing in sample 5, right here:
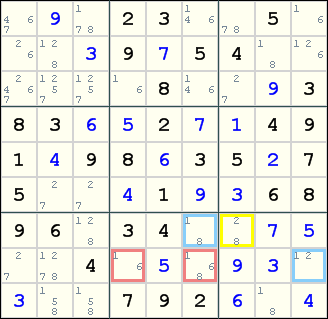
With XY-Wing disabled, this is the finned X-Wing, as you pointed out:
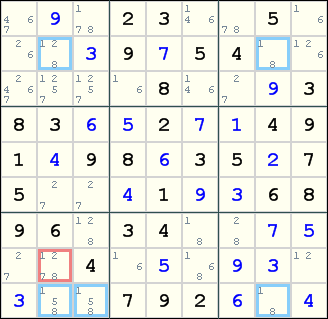
And now... something completely different...
Now the we have a lot of examples, let's talk about the way to locate them in the grid (from quite a long distance away). All the samples I've seen so far place them in 4 different boxes. Is that a coincidence, or a prerequisite? Any other limitations that I can exploit?
Ruud. |
|
| Back to top |
|
 |
| rkral
| | Joined: 21 Oct 2005 | | Posts: 233 | | : | |
Items |
|
 Posted: Sat Mar 11, 2006 7:22 pm Post subject: Posted: Sat Mar 11, 2006 7:22 pm Post subject: |
 |
|
| Ruud wrote: | | All the samples I've seen so far place them in 4 different boxes. Is that a coincidence, or a prerequisite? |
The following seems theoretically possible ... | Code: |
. - .|. . .|. + .
. x .|. . .|# x #
. x .|. . .|# x #
-----+-----+-----
. - .|. . .|. - .
. - .|. . .|. - .
. - .|. . .|. - .
-----+-----+-----
. - .|. . .|. - .
. - .|. . .|. - .
. - .|. . .|. - . |
... but is obliterated by line-box interaction, I suppose.
| Ruud wrote: | | Now the we have a lot of examples, let's talk about the way to locate them in the grid (from quite a long distance away). |
"from a long distance away" 
Ron |
|
| Back to top |
|
 |
| Ruud
Site Admin
 | | Joined: 17 Sep 2005 | | Posts: 708 | | : | | Location: Netherlands |
Items |
|
|
| Back to top |
|
 |
| tarek
| | Joined: 31 Dec 2005 | | Posts: 153 | | : | | Location: London, UK |
Items |
|
 Posted: Sat Mar 11, 2006 11:51 pm Post subject: Posted: Sat Mar 11, 2006 11:51 pm Post subject: |
 |
|
I programmed my solver to spot finned fishes (including the sashimi variation) up to to level of squirmbag........The long way I'm afraid...
It is basically like you would explain it to a human.........
Observation 1: The finned x-wing closely resembles the x-wing.......remove the fins & you get an x-wing
an x-wing has exactly 4 cells in 2 rows & 2 columns
You can have a maximum of Two fins (cells) in a finned x-wing.
so: (I'm not too good in pseudo code, the following assumes that the fish is in columns eliminating in rows, swap columns with rows to get the opposite)
1st filter: fish (n=2 x-wing, n=3 swordfish, .........)
2nd filter: Number of cells in a finned fish "Min:(n*2)+1 Max:(n*n)+2" cells in n columns & (n+1 rows or n+2 rows)
3rd filter: Only one column has >n*n cells
observation 2: All Fin(s) should share a box with at least one vertix
4th filter: combining observations 1 & 2
In Only one box would removal of (1-2) cells lead to an n-true fish
---Now you should have a finned n fish, that can eliminate in vertices rows only in the box containing the fin(s). [Note: if you have a mixed normal pattern with a sashimi pattern, this step can combine them easily]
example of the mixed pattern finned swordfish: | Code: | . . .|. . .|. . .
. . .|. . .|. . .
. X X|. X .|. . .
-----+-----+-----
. * *|. . .|. . .
. . *|. . .|. . .
F . X|. X .|. . .
-----+-----+-----
. . .|. . .|. . .
. X .|. X .|. . .
. . .|. . .|. . . |
for the pure sashimi variation it is a BIT more complicated......because you may have several sashimi formations using the same cells......
Tarek |
|
| Back to top |
|
 |
| Ruud
Site Admin
 | | Joined: 17 Sep 2005 | | Posts: 708 | | : | | Location: Netherlands |
Items |
|
 Posted: Sun Mar 12, 2006 4:56 pm Post subject: Posted: Sun Mar 12, 2006 4:56 pm Post subject: |
 |
|
Thanks Tarek, for your insights.
I now think it is possible to write a generic function to search for N-sized finned formations.
The only irregularity is in the row/column containing the fin. The other rows/columns can be found by the same method as if you were looking for a regular N-sized fish.
So, when we find N-1 rows with a total of N candidates (where N>=2):
then we go look for a row that has at least one candidate in of the columns found in the 'regular' rows, and at least 1 extra candidate in the same tower as one of the other columns.
This method would cover every size and both normal finned and sashimi variations, I think.
Any comments?
Ruud. |
|
| Back to top |
|
 |
| rkral
| | Joined: 21 Oct 2005 | | Posts: 233 | | : | |
Items |
|
 Posted: Sun Mar 12, 2006 7:06 pm Post subject: Posted: Sun Mar 12, 2006 7:06 pm Post subject: |
 |
|
| Ruud wrote: | So, when we find N-1 rows with a total of N candidates (where N>=2):
then we go look for a row that has at least one candidate in of the columns found in the 'regular' rows, and at least 1 extra candidate in the same tower as one of the other columns.
This method would cover every size and both normal finned and sashimi variations, I think.
Any comments? |
First, your "at least 1 extra candidate in the same tower ..." probably should read "at least 1 extra candidate in exactly one tower ...".
Second, I hadn't noticed that the "filled cell" of the sashimi was always in the same box as the fins ... but that clearly has to be the case.
Third, the part I've yet to figure out is how to write the generic body of code that handles different N ... because of the different number of loops. I sure would appreciate a clue there.
TIA, Ron |
|
| Back to top |
|
 |
|
|
You cannot post new topics in this forum
You cannot reply to topics in this forum
You cannot edit your posts in this forum
You cannot delete your posts in this forum
You cannot vote in polls in this forum
|

Powered by phpBB © 2001, 2005 phpBB Group
Igloo Theme Version 1.0 :: Created By: Andrew Charron |







